Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 87
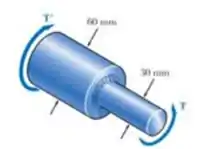
O eixo seção variável mostrado na figura deve rotacionar com uma frequência de 50Hz. Sabendo que o raio do adoçamento é e que a tensão de cisalhamento admissível é de MPa, determine a potência máxima que pode ser transmitida.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a frequência mínima na qual o eixo pode girar. Comecemos trazendo alguns dados e conversões:
Considerando K, podemos então verificar o torque permitido:
Ufa, chegamos ao cálculo da força máxima:
Resposta
Então gurizada, temos o nosso resultado, a potência máxima é:
Exercícios de Livros Relacionados
Sabendo-se que a tensão de cisalhamento admissível é de 55M P a para o eixo escalonado mostrado, determinar a intensidade T do maior torque que pode ser transmitido pelo eixo, quando o raio de adoçame
Sabendo-se que o eixo escalonado mostrado transmite um torque de intensidade T = 280N ⋅ m , determinar a máxima tensão de cisalhamento no eixo, quando o raio de adoçamento é: (b)r = 4 , 8m m
Um tubo de parede fina foi fabricado pelo encurvamento de uma placa de metal, espessura t, onde suas bordas foram unidas de tal modo que tomasse a forma de um cilindro de raio c. Um torque T é então a
Resolver o prob. 3.132 assumindo que a placa de metal tenha sido dobrada na forma de um tubo de seção transversal quadrada de lado c.
Um eixo cilíndrico vazado de comprimento L, raio médio c m e espessura uniforme t , está submetido aos torques de intensidade T . Considerar inicialmente os valores da tensão média de cisalhamento τ m