Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 40
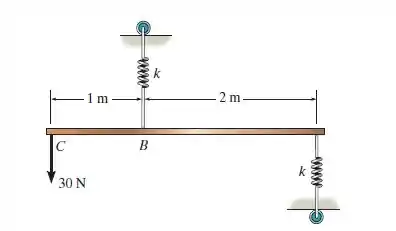
Um elemento horizontal de peso desprezível é apoiado por duas molas, cada uma com rigidez . Se as molas estiverem inicialmente não esticadas e a força for vertical, conforme mostrado, determine o ângulo que o elemento forma com a horizontal, quando a força de é aplicada.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar o ângulo de inclinação da barra com a horizontal.
Para isto, será fundamental determinarmos a deformação de cada uma das molas na direção vertical, o que necessitará que calculemos as forças sobre cada uma das molas, visto que a deformação é:
Assim, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Então, o nosso diagrama de equilíbrio será:
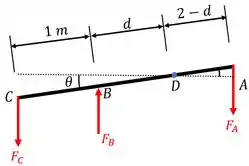
Um ponto importante para esta questão é como a barra se movimenta em após a aplicação da . Esta é uma força que faz com que a barra tenda descer. Já as molas tendem segurar a barra, mantendo-a elevada. Então é fácil ver que a barra irá rotacionar no sentido horário.
Por causa disto, a nossa barra irá rotacionar em torno de um ponto que fica entre a aplicação das forças das duas molas.
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar calculando a força . Para isto, temos que calcular o somatório do momento em relação ao ponto , pois assim eliminamos a força , que ainda é uma incógnita da nossa equação.
Desta forma, temos:
E assim encontramos a nossa primeira força!
Passo 3
Para determinarmos a força na outra mola, basta fazermos o somatório de forças na direção vertical. Desta forma, temos:
E assim determinarmos as forças nas duas molas!
Passo 4
Para podermos determinar o ângulo de inclinação é necessário determinarmos a deformação de cada uma das molas. Aplicando a equação para cada uma das molas, temos:
Com a informação da deformação podemos calcular aonde está o ponto . Isto é, a distância do nosso diagrama de equilíbrio. Pela relação geométrica, temos:
E então, o nosso ângulo é:
E assim finalizamos a questão!