Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 26
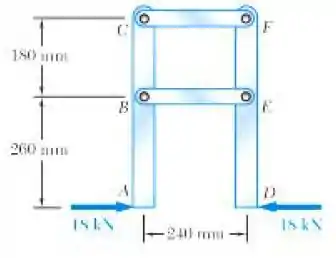
Os elementos ABC e DEF são unidos por barras de conexão de aço . Cada uma dessas barras é feita de um par de placas de 25 x 35 mm. Determine a mudança de comprimento do (a) elemento BE, (b) elemento CF.
Passo 1
Fala aí gurizada tudo belezinha? Antes de tudo que tal esboçarmos um diagrama de corpo livre do elemento ABC, mas já vamos deixar em metros para facilitar os cálculos posteriores:
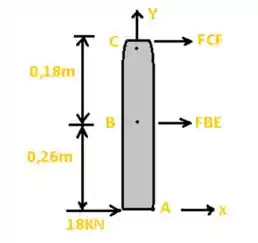
Agora podemos começar calculando o somatório do momento em B:
E agora gurizada o somatório de forças em “x”.....
Agora para que possamos calcular o alongamento precisamos antes encontrar a área
Passo 2
Agora sim partiu encontrar o alongamento das seções
Resposta
Exercícios de Livros Relacionados
Um vaso de pressão de 300mm de diâmetro externo é fabricado com chapa de aço de 6,35mm de espessura, que é soldada ao longo de uma hélice formando um ângulo de 22,5 ° com a horizontal. Sabendo-se que
Resolver o P r o b . 6.111 , assumindo que a força P é horizontal ( α = 0 ) Ponto k;
Resolver o P r o b . 6.111 , assumindo que a força P é horizontal ( α = 0 ) Ponto L;
O tanque de ar comprimido A B tem um diâmetro externo de 250 m m e uma espessura de 8m m . Nele é montado um colar, no qual uma força P de 40 k N pode ser aplicado em B , formando um ângulo α = 30 ° c
O tanque de ar comprimido A B tem um diâmetro externo de 250 m m e uma espessura de 8m m . Nele é montado um colar, no qual uma força P de 40 k N pode ser aplicado em B , formando um ângulo α = 30 ° c