Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 96

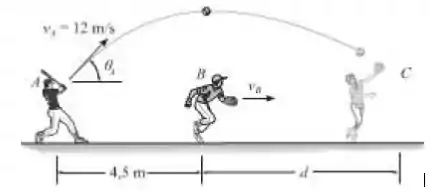
O jogador de beisebol A rebate a bola com v A = 12   m / s e θ A = 60 ° . Quando a bola está diretamente acima do jogador B, ele começa a correr embaixo dela. Determine a velocidade escalar constante v B e a distância d na qual B tem de correr a fim de segurar a bola na mesma altura a qual ela foi rebatida.

Passo 1

Temos um problema de movimento oblíquo, o movimento de um projétil. A bola rebatida por A se desloca em todo um plano x y . Para descobrirmos a sua velocidade em cada um dos eixos precisamos fazer a decomposição da sua velocidade. Sendo assim,

v A x = v A ⋅ cos ⁡ θ A

v A y = v A ⋅ sen ⁡ θ A

A diferença entre ambas as componentes é que, na direção do eixo x , a velocidade é constante. Já na direção do eixo y , temos a ação da gravidade! Muito cuidado para não esquecer dela!

Portanto, para resolvermos esta questão, precisamos descobrir o tempo necessário para a bola voltar a sua coordenada y original (zero), e com este valor descobriremos o caminho percorrido pela bola no eixo x . Consequentemente, obteremos o valor da distância d que o jogador B precisa percorrer. Em relação a velocidade, discutiremos posteriormente. Vamos as contas então!

Passo 2

Vamos começar determinando o tempo t da trajetória da bola! Suponha que a bola começa a uma altura s 0 = k . Como ela retorna a mesma altura, então, a sua posição final será s = k . Sabendo que a trajetória em y está sujeita a ação da gravidade, a partir das equações da cinemática, teremos:

s = s 0 + v y t + a t 2 2

Como v y = v A y , temos:

k = k + v A ⋅ sen ⁡ 60 ° ⋅ t - g t 2 2

0 = 6 3 t - 4,905 ⋅ t 2

Resolvendo esta equação do segundo grau, obtemos t 1 = 0 ou t 2 = 2,12   s . Como o tempo t 1 implica que não houve passagem do tempo, a nossa resposta será t 2 !

Passo 3

Agora que descobrimos o tempo que a bola necessita para subir e retornar à sua altura, vamos calcular a distância percorrida no eixo x . Como neste eixo ela possui velocidade constante, temos:

s = s 0 + v 0 t

s = 0 + v A x t 2

s = 12 ⋅ cos ⁡ 60 ° ⋅ 2,12

s = 12,72   m

Portanto, o valor da distância d que o jogador B precisa percorrer é:

d = s - 4,5 = 8,22   m

Passo 4

Em relação a velocidade do jogador B, o seu valor é exatamente igual a componente v A X = 6   m / s . Como ele começa a correr com velocidade constante apenas a partir do momento em que a bola está acima dele, ele precisa percorrer a mesma distância no mesmo tempo que a bola. Portanto, ambos possuem a mesma velocidade.

Resposta

d = 8,22   m

v B = 6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é lançado com uma velocidade inicial de 200m / s em um ângulo de 60 ° em relação à horizontal. Calcule o alcance R medido para acima da inclinação.
Se o jogador de tênis dá o saque horizontalmente ( θ = 0 ) , calcule sua velocidade v se o centro da bola transpõe a rede de 0,9m por 150m m . Encontre também a distância s a partir da rede até o pont
Um projétil é disparado com uma velocidade u na entrada A de um túnel horizontal de comprimento L e altura H . Determine o valor mínimo de u e o valor correspondente do ângulo θ para o qual o projétil
Um projétil é disparado com uma velocidade u perpendicular ao declive, que está inclinado de um ângulo θ com a horizontal. Derive uma expressão para a distância R até o ponto de impacto.
Determine a localização h do ponto em direção ao qual o arremessador deve lançar a bola de modo que ela atinja a mão do receptor. A bola é lançada com uma velocidade de 40m / s .