Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 25

A bobina tem uma massa de 100 kg e raio de giração de 400 mm em relação a seu centro de massa O. Se ela é liberada do repouso, determine sua velocidade angular após seu centro O haver descido pelo plano uma distância de 2 m. A superfície de contato entre a bobina e o plano inclinado é lisa.

Passo 1

Começaremos o exercício calculando a velocidade do centro de massa em função da velocidade angular da bobina

v O = ω r O = ω 0 , 3

Agora iremos calcular o momento de inércia da bobina em relação ao seu centro de massa:

I O = m k O 2 = 100 0,4 2 → I G = 16   k g . m 2

Sendo assim, a energia cinética do sistema é dada por:

T = 1 2 I O ω 2 + 1 2 m v O 2

T = 1 2 16 ω 2 + 1 2 100 ω 0,3 2

T = 12,5 ω 2

Passo 2

Como o sistema está inicialmente em repouso, T 1 = 0 . Através da analise da figura a seguir:

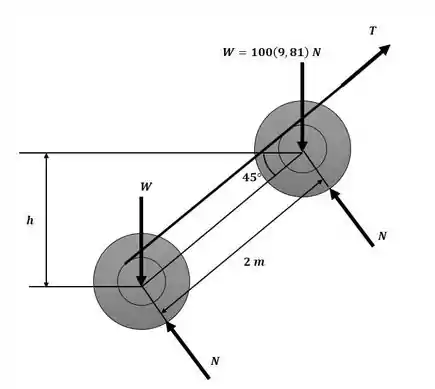
Sabemos que T e N não realizam trabalho, equanto W realiza. Sendo assim, quando o centro da bobina se move uma distância de s O = 2   m :

h = s O c o s 45 ° = 1,4142   m

Sendo assim, o trabalho feito por W é:

U W = W h = 100 9,81 1,4142 → U W = 1387,34   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 1387,34 = 12,5 ω 2

ω = 10,5   r a d / s

Resposta

ω = 10,5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo apresentado é construído de uma haste esbelta uniforme e consiste em um anel de raio r fixado a uma seção reta de comprimento 2 r . O corpo se articula livremente em relação a uma junta esféri
A roda dupla de 10k g , com raio de giração de 125m m em relação a O , está ligada à mola de rigidez k = 600 N / m por um fio que está enrolado firmemente em torno do eixo central. Se a roda é liberad
A estrutura quadrada vazada é construída com quatro hastes esbeltas idênticas, cada uma de comprimento b . Se a estrutura é liberada a partir do repouso na posição mostrada, determine a velocidade do
A figura mostra a seção transversal de uma porta de garagem de 100k g , que é um painel retangular uniforme de 2,4m por 2,4m . A porta movimenta dois conjuntos de molas, um em cada lado da porta, tal
O semicilindro maciço homogêneo é liberado a partir do repouso na posição indicada. Se o atrito é suficiente para evitar o deslizamento, determine a velocidade angular máxima ω atingida pelo cilindro