Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 83
A engrenagem gira a polia para correias em a uma velocidade constante. Para as forças trativas mostradas na correia, calcule a força no dente da engrenagem e os módulos das forças totais suportadas pelos mancais em e .
c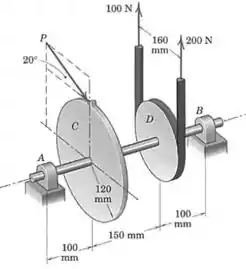
Passo 1
Vamos começar definindo eixos de coordenadas:
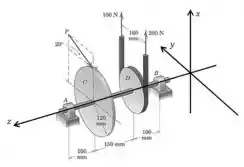
E as forças que atuam no sistema são as seguinte: a força na engrenagem , as duas forças de e na engrenagem , e as componentes , , e das forças em e (essas forças não têm componentes na direção do eixo ).
Passo 2
Agora vamos usar algumas equações de equilíbrio para resolver o problema. Começamos com o equilíbrio dos momentos em relação ao eixo , pois como nesse caso os momentos de todas as forças em e são nulos, deve ser a expressão mais simples.
A componente em da força cruza o eixo , então também não possui momento. Ficamos então com a componente da força e as duas forças que atuam na engrenagem .
Sendo assim, considerando o sentido anti-horário como positivo, teremos:
Esse é nosso primeiro resultado.
Passo 3
Agora vamos analisar o sistema no plano , isso vai simplificar bastante as coisas (pense nisso como a vista “de cima” do nosso desenho). E dentro desse plano, vamos calcular o momento em relação ao ponto .
Nesse plano vemos apenas as forças , e uma componente da força . Como está sobre nosso ponto de referência, o seu momento é nulo:
E ainda nesse plano, vamos considerar o equilíbrio na direção do eixo :
Ótimo, encontramos as duas componentes em . Agora vamos analisar outro plano para obter as componentes em .
Passo 4
Vamos analisar o plano , pense nisso como a vista “de lado” do sistema, e mais uma vez vamos usar o equilíbrio de momento em relação a .
Nesse plano aparecem as forças de e , a outra componente da força , e as componentes e das forças nos mancais.
E mais uma vez, agora vamos usar o equilíbrio das forças na direção do eixo , ainda nesse plano:
E agora podemos calcular os módulos das duas forças:
Resposta
E então os módulos das forças são , e .