Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 107
Um torque aplicado a uma barra maciça feita de um material elastoplástico é aumentado até que a barra se torne completamente plástica, e então é removida:
- Mostrar que a distribuição de tensões residuais são as representadas na figura;
- Determinar a intensidade do torque, devido as tensões atuantes na torção da barra localizada dentro de um círculo de raio .
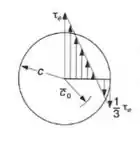
Passo 1
Sabemos que o nosso desenho pode ser pensado da seguinte maneira:
- Temos as tensões quando a estrutura é carregada:
- Temos as tensões quando a estrutura é descarregada:
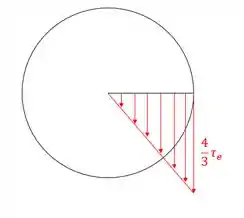
Juntando os dois teremos que:
Passo 2
Fazendo o cálculo depois de carregarmos (que é o primeiro círculo do nosso desenho ali em cima), temos que a fórmula para cálculo do torque é dado pela seguinte equação.
E veja que ,ou seja, podemos afirmar que o núcleo elástico é dado por:
Sendo assim teremos que:
Descarregando teremos que a tensão cisalhante será calculada da maneira que já conhecemos, sendo assim teremos que:
E já sabemos qual a fórmula do nosso torque, se substituirmos, teremos que:
Sendo assim temos que a tensão residual é dada por:
Supondo que teremos que:
Passo 3
Definindo por um raio de tamanho , podemos fazer a nossa equação da seguinte maneira, calculando o nosso torque pela seguinte integral:
Calculando a nossa tensão residual total teremos que, usando não mais o macete .
Substituindo na nossa integral teremos que:
Colocando o em função do C, teremos que:
Considerando a tensão residual igual a zero e , teremos que:
Resolvendo a nossa integral teremos que:
Substituindo teremos que: