Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 16

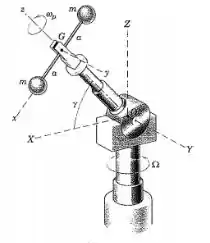
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . Determine a aceleração angular do haltere. O conjunto inteiro gira em torno do eixo vertical Z com Ω aumentando na taxa de 3 rad/s² para o instante considerado e   Ω 0 = 0,8   r a d / s .

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que esse haltere doidão tem o eixo rodando a uma velocidade constante e que o eixo também está rodando, e nos pede a aceleração angular. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??

Passo 2

Nosso primeiro passo será determinar nossas variáveis e a aceleração inicial do nosso sistema.

Ω 0 = 0,8   r a d / s   Ω ˙ = 3   r a d / s ²  

α ' = ω p   x   Ω = 0,8 c o s 30 ° k - s e n 30 ° i x   2 k = 0,8 j   r a d / s ²

Passo 3

Pronto!! Com isso, podemos achar qual a nossa aceleração angular.

α =   Ω   x   ω p + Ω ˙ α = 0,8 j + 3 ( c o s 30 ° k - s e n 30 ° i ) α = - 1,5 i +   0,8 j + 2,6 k   r a d / s ²

Resposta

α = - 1,5 i +   0,8 j + 2,6 k   r a d / s ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

123. O disco circular maciço de massa m e pequena espessura está girando livremente sobre seu eixo à taxa p . Se o conjunto é liberado na posição vertical em θ = 0 com θ ˙ = 0 , determine as component
106. As pás e o cubo do rotor do helicóptero têm uma massa de 64k g e um raio de giração de 3,0m em relação ao eixo de rotação z . Com o rotor girando a 500r p m durante um curto intervalo após a deco
98. A estudante se ofereceu voluntariamente para auxiliar em uma demonstração na sala de aula envolvendo uma roda com quantidade de movimento, que está girando rapidamente com velocidade angular p com
102. Um ônibus ecológico experimental é acionado pela energia cinética armazenada em um grande volante que gira a uma alta velocidade p no sentido indicado. Quando o ônibus encontra uma pequena rampa
101. Um aeroplano acaba de deixar a pista com uma velocidade de decolagem v . Cada uma de suas rodas que gira livremente possui uma massa m , com um raio de giração k em relação ao seu eixo. Quando ob