Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 22

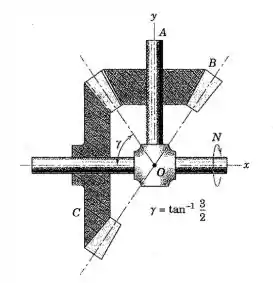
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone primitivo com semi-ângulo de vértice γ = t g - 1 3 2 como mostrado. Determine a velocidade angular w e a aceleração angular α da engrenagem B, se a engrenagem C é fixa e não gira. O eixo y gira com a árvore AO.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que esse monte de engrenagem tem o eixo rodando a uma velocidade constante e que o eixo não está rodando, e nos pede a velocidade e a aceleração angulares. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??

Passo 2

Nosso primeiro passo será determinar nossa velocidade escalar no centro da engrenagem B. Como sabemos que a extremidade de B está ligada à engrenagem C, sabemos que a velocidade escalar naquele ponto será zero.

V   =   3 b 3 b 2   60   2 π 60 = 3 π b

w y =   V b = 3 π   r a d / s

w x = - 60   2 π 60 = - 2 π   r a d / s

w =   - 2 π   i + 3 π   j   r a d / s

Passo 3

Pronto!! Com isso, podemos achar qual a nossa aceleração.

α =   w ˙  

i   ˙ = 0

j ˙ = w   x   j =   - 2 π   k

α =   - 6 π 2 k   r a d / s ²

Resposta

w =   - 2 π   i + 3 π   j   r a d / s

α =   - 6 π 2 k   r a d / s ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Coloque o seu livro sobre sua mesa, com eixos fixos orientados como indicado. Gire o livro em torno do eixo x através de um ângulo 90º e, em seguida, a partir dessa nova posição gire-o 90º em torno do
O robô do Prob. 7/17 é apresentado novamente aqui, onde o sistema de coordenadas x - y - z com origem em O 2 gira em torno do eixo X na velocidade angular θ ˙ . Os eixos sem rotação X - Y - Z orientad
109. Cada uma das rodas idênticas tem uma massa de 4 k g e um raio de giração k z = 120 m m e está montada a uma haste horizontal A B presa à haste vertical em O . No caso (a), a a haste horizontal es
95. O avião a jato na parte inferior de uma acrobacia aérea na forma de um círculo em um plano vertical, tem uma tendência, devido a ação giroscópica do rotor do motor, a mudar de direção para a direi
110. Se a roda no caso (a) do problema 7 / 109 é forçada a executar uma precessão em torno da vertical, por um acionamento mecânico na taxa constante de Ω = 2 j ^r a d / s , determine o momento fletor