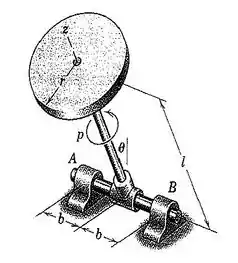
123. O disco circular maciço de massa e pequena espessura está girando livremente sobre seu eixo à taxa . Se o conjunto é liberado na posição vertical em com , determine as componentes horizontais das forças e exercidas pelos respectivos mancais sobre o eixo horizontal quando a posição é atingida. Despreze a massa dos dois eixos em comparação com e despreze todo o atrito. Resolva utilizandos as equações de momento apropriadas.
Passo 1
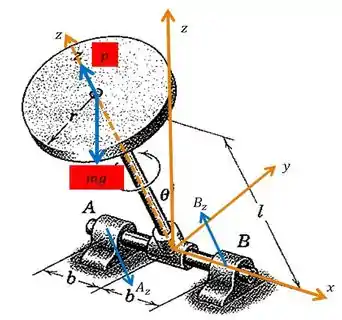
Primeiramente vamos fazer a representação do nosso sistema, posicionando-o em três eixos coordenados de forma a auxiliar nossa interpretação:
Passo 2
Uma vez que do enunciado, tiramos que a velocidade de precessão terá o seguinte valor:
E sua derivada, consequentemente:
Como podemos ver na figura que esboçamos, temos que fazer o somatório dos momentos em relação a três direções. Como já obtemos que a velocidade de precessão e sua derivada, valem zero, as equações de momento da parte podem ser simplificadas como:
Logo, primeiro para a direção em , temos que:
E qual é mesmo o momento que está presente no eixo ? Bem! Se olharmos a figura do , veremos que a única forca que gera momento nesse eixo é o peso , de forma que o momento resultante é o produto da força pela distância . Em relação ao momento de inércia, como o eixo é paralelo ao disco e está a uma distância desse eixo temos então a seguinte relação:
é o nosso , dado por:
Agora para a direção , façamos:
No eixo , as coisas são bem diferentes porque o momento está sendo gerado pelas forças de reação e , que estão a uma distância desse eixo, de modo que ficamos com:
Ahhhh! é o nosso momento , que é dado por:
Finalmente, façamos o somatório de momentos no eixo . A grande questão é que momentos são esses, uma vez que não estão agindo nenhum nesse eixo. Ficamos então, com:
Já que obviamente vai existir um momento de inércia em relação ao eixo , e ele existe, sendo igual a , temos que a única possibilidade do momento em dar zero é que:
Passo 3
Agora, usemos a seguinte relação:
E se temos diferencial nos dois lados, partiu usar a integral. Como a integral do diferencial tende a nos fornecer um ângulo, vamos usar os limites de integração variando de até como diz a questão. Para a aprte da relação com o diferencial , temos que usar os limites de integração variando de até , que é o ângulo que a integração desse diferencial tende a fornecer:
Mas do , sabemos que:
Logo, substituindo esse valor na integral, obtemos que:
Voltemos então, à seguinte relação que obtivemos no :
E também para , façamos o somatório das forças na direção :
Combinando em seguida, as duas equações anteriores, obtemos o sistema:
Somando e , alcançamos que:
Substituindo em seguida, na equação , obtemos o valor de como:
E não podemos nos esquecer que:
E consequentemente: