Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 68
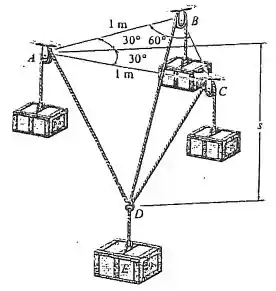
Os três blocos mais externos têm massa de 2 kg cada um e o bloco central E tem massa de 3 kg. Determine a distância s para o equilíbrio do sistema.
Passo 1
Para encontrar a distância , o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
Como o triângulo ABC é equilátero, ou seja, possui lados de mesma medida, então
Tem-se que a caixa E exerce uma força peso, tal que
E como os blocos são mantidos pelas suas próprias cordas, teremos que as tensões nas cordas serão iguais aos seus pesos:
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
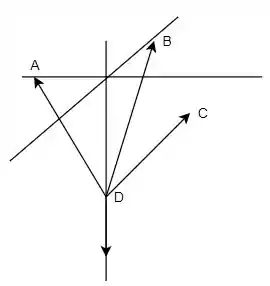
Agora o tringulo que podemos desenhar em uma corda:
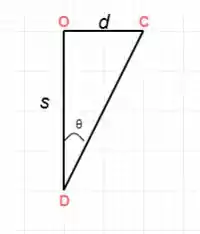
Em que O é o centro do diagrama de forças.
Vamos então utilizar a equação do equilíbrio ao longo do eixo :
Temos então:
Substituindo os valores:
Juntando todo mundo:
Teremos então:
E consequentemente:
Passo 3
Levando então o triangulo que criamos:
E