Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 97
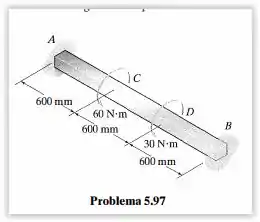
Uma escora de alumínio está presa entre duas paredes e . Se tiver seção transversal quadrada de por e for submetida ao carregamento de torção mostrado, determine as reações nos apoios fixos. Determine também o ângulo de torção em .
Passo 1
Olá pessoal! Tudo bem?
Nosso objetivo nessa questão é achar as reações nos apoios fixos e . O enunciado informa que a viga tem seção transversal quadrada de por , ou seja, . O material é alumínio, então o módulo de elasticidade transversal é .
Observando a figura do enunciado vamos fazer os cortes nas seções para posteriormente fazer o equilíbrio da viga.
Fazendo o somatório dos momentos, temos:
Na seção :
Na seção :
Na seção :
Observe que .
E como é uma viga engastada nos dois lados, . Analisando as seções da viga de para , temos que:
Sendo que o ângulo de torção para vigas de seção transversal quadrada é calculado através da equação:
OBS: Na tabela do Hibeller essa fórmula está com um erro, falta multiplicar por .
Passo 2
Através do ângulo de torção , vamos determinar o torque em . Usaremos os torques que obtivemos no somatório dos momentos para cada seção, que estão todos em função de .
Passo 3
Agora é só substituir na relação que obtivemos no somatório do Passo 1.