Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas de Revisão - Ex. 192

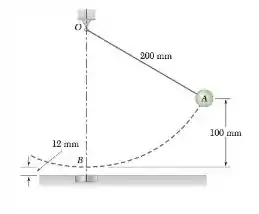
Uma esfera de aço de 50 g é presa a uma corda de 200 mm que pode balançar em volta do ponto O no plano vertical. Ela está sujeita a seu próprio peso e a uma força F exercida por um pequeno ímã incorporado ao chão. A intensidade dessa força, expressa em newtons, é F = 0,00024/r2, onde r é a distância entre o ímã e a esfera expressa em milímetros. Sabendo que a esfera é liberada do repouso em A, determine sua velocidade quando ela passa pelo ponto B.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual é a velocidade. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, vamos determinar a velocidade quando passa por B através da conservação de energia:

r 1 2 = 100 + 12 2 + 200 2 - 200 - 100 2

r 1 = 206 ,   26   m m

V m 1 =   - F r 1

V m 1 = - 0,0000011

V g 1 = W 100 + 12

V g 1 = 14   m m

Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.

V 1 = 13,999   m m

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

T 1 = 0

T 2 = 0,00119409   v B ²

V 2 = - 1,49998   m m

Com a conservação de energia, chegamos na seguinte equação:

0 + 13,999 = 0,00119409   v B 2 - 1,49998

v B = 0,08   m / s

Resposta

v B = 0,08   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O projeto para uma nova prótese de quadril está sendo estudado usando um instrumento de inserção e um fêmur fixo falso. Considerando que o punção aplica uma força média de 2 kN durante um tempo de 2 m
A última parte da prova de salto triplo do atletismo é o salto final, em que o atleta faz o último salto e aterrissa em uma caixa de areia. Considerando que a velocidade de um atleta de 90 kg justamen
O seguinte modelo matemático foi sugerido para a variação na pressão dentro do diâmetro de 10 mm do cano de um rifle quando uma bala de 25 g é disparada: p t = 950M P a e - t / ( 0,16m s ) onde t é ex
Uma estimativa da carga esperada sobre cintos de segurança é feita antes de se desenhar protótipos de cintos que serão avaliados em testes de impacto com automóveis. Admitindo que um automóvel que rod
Um modelo simplificado baseado em uma linha reta deve ser obtido para a variação de pressão dentro do cano de um rifle de 10 mm de diâmetro durante o disparo de uma bala de 20 g. Sabendo que leva 1,6