Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 17
Uma partícula viajando em uma linha reta encontra uma força que a retarda e provoca a redução de sua velocidade segundo , onde é o tempo em segundos durante o qual a força age. Determine a aceleração da partícula quando e encontre a distância correspondente que a partícula se deslocou durante o intervalo de segundos. Faça o gráfico de em função de para os primeiros segundos.
Passo 1
O enunciado já deu a função da velocidade:
E o primeiro objetivo é determinar a aceleração da partícula em . Precisamos lembrar da seguinte relação:
E no instante vamos ficar com o seguinte resultado:
Passo 2
O próximo objetivo é encontrar a distância que a partícula percorre nesses primeiros segundos. Vamos lembrar do seguinte:
Substituindo com a função da velocidade:
E Integrando os dois lados:
Passo 3
Agora precisamos esboçar um gráfico da velocidade em função do tempo para esses primeiros segundos.
Para resolver a questão numericamente, deve ser suficiente calcular a função em mais ou menos cinco pontos:
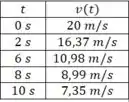
E posicionando esses pontos no plano, o resultado deve ser algo parecido com isso:
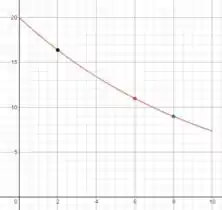
O essencial aqui é notar que o gráfico não se aproxima muito do eixo , e que tem um decaimento quase linear, porque a divisão por dez na exponencial deixa o decaimento mais lento.
Resposta
A aceleração da partícula é e o deslocamento é .