Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 239

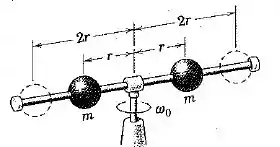
As duas esferas de massas iguais m podem deslizar ao longo da haste horizontal que gira. Se elas estão inicialmente travadas na posição a uma distância r do eixo de rotação com o conjunto girando livremente com uma velocidade angular ω 0 , determine a nova velocidade angular ω após as esferas serem liberadas e finalmente assumirem posições nas extremidades da haste na distância radial de 2 r . Encontre também a fração n da energia cinética inicial do sistema que é perdida. Despreze a pequena massa da massa da haste e do eixo.

Passo 1

Bom galera, nesse exercício queremos encontrar a velocidade angular ω e a taxa de energia cinética perdida. Como a quantidade de movimento angular se conserva, temos

Δ H = 0

Passo 2

Podemos então escrever

2 m r ω 0 r - 2 m 2 r ω 2 r = 0

Isolando ω , temos

ω = ω 0 4

Passo 3

Para a perda de energia, sabemos que   n = Δ T T . Δ T pode ser expressado por

Δ T = 2 1 2 m r ω 0 2 - 2 1 2 m 2 r ω 0 4   2 = 3 m r 2 ω 0 2 4

Substituindo em n , temos

n = Δ T T = 3 m r 2 ω 0 2 4 m r 2 ω 0 2 = 3 4

Resposta

ω = ω 0 4

n = 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A cúpula hemisférica de massa m é mantida em equilíbrio pelo jato vertical de água descarregado por um bocal de diâmetro d . Se a descarga de água através do bocal é Q , determine a altura h a que a c
O escoadouro é usado para desviar o curso da água, Q = 0,6m 3 / s . Se a água tem uma área de seção transversal de 0,05m 2 , determine as componentes da força, no pino D e no rolete C , necessárias pa
Uma lancha é propelida pelo motor a jato mostrado na figura. A água do mar é puxada pela bomba, a uma vazão de 0,54m 3 / s , através de uma entrada A , de 150m m de diâmetro. Uma hélice acelera a vazã
O pêndulo consiste de uma esfera de 5k g e uma barra de 2k g . Se ele é solto do repouso quando θ = 90 ° , determine o ãngulo θ de repique após a esfera bater no chão. Considere e = 0,8 .
O centro de massa da bola de 1,5k g tem uma velocidade v G 1 = 1,8m / s quando ela acerta a extremidade da barra fina lisa de 2,5k g que está em repouso. Determine a velocidade angular da barra em tor