Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 245
No ponto de maior aproximação com o Sol, um cometa tem uma velocidade . Determine as componentes radial e transversal de sua velocidade no ponto B, onde a distância radial a partir do Sol é .
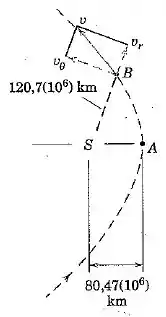
Passo 1
Bom galera, nesse exercício queremos determinar as componentes da velocidade no ponto . Pela conservação do momento angular, temos que
Passo 2
Substituindo, temos
Isolando , temos
Utilizando a conservação de energia, temos
Passo 3
Substituindo, temos
Substituindo os valores, temos
Sabemos que a velocidade radial é
Resposta
Exercícios de Livros Relacionados
O carro de 75k g , de uma atração de parque de diversões, está conectado a uma lança telescópica giratória. Quando r = 4,5m , o carro move-se em uma trajetória horizontal circular a uma velocidade de
Um satélite de massa 700k g é lançado em uma trajetória de voo livre em torno da Terra a uma velocidade inicial v A = 10k m / s , quando a distância do centro da Terra é r A = 15M m . Se o ângulo de l
No instante que r = 1,5m , ao disco de 5k g é dada uma velocidade v = 5 m / s , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante r
A bola de 2k g gira em torno de uma trajetória circular de 0,5m de diâmetro com velocidade constante. Se o comprimento da corda é encurtado de l = 1m até l ' = 0,5m , puxando-se a corda através do tub
Quando se dá ao pêndulo de 2k g uma velocidade horizontal de 1,5m / s , ele começa a girar em torno da trajetória circular horizontal A . Se a força F na corda é aumentada, o pêndulo sobe, e então gir