Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 155
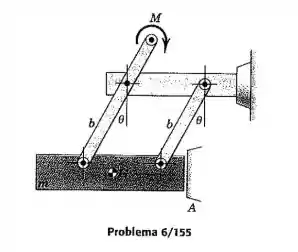
A carga de massa é suportada pelas hastes leves paralelas e pelo batente fixo . Determine a aceleração angular inicial das barras devido à aplicação do momento a uma extremidade como mostrado.
Passo 1
A variação da eneria cinética do sistema é dada por
Lembrando que
Isolando , temos
Substituindo na expressão para dT, obtemos
Já a variação da eneria potencial gravitacional do sistema é dada por
Passo 2
Sabemos que para um intervalo infinitesimal de movimento, a relação Trabalho-Energia é dada por
Além disso, para rotações finitas
Igualando as duas equações, ficamos com
Substituindo as expressões encontradas,
Isolando a aceleração angular , achamos
Resposta
Exercícios de Livros Relacionados
O carro de massa m acelera em uma estrada horizontal sob a ação da força motriz F de uma velocidade v 1 até uma velocidade mais alta v 2 em uma distância s . Se o motor desenvolve uma potência de saíd
O bloco de 10k g é liberado a partir do repouso sobre a superfície no ponto B , onde a mola foi esticada por uma distância de 0,5m a partir de sua posição neutra A . O coeficiente de atrito dinâmico e
Um menino de 40k g parte do repouso na base A de uma inclinação de 10 % e aumenta sua velocidade em uma taxa constante até 8k m / h quando passa em B , 15m ao longo da inclinação a partir de A . Deter
Um carro está viajando a 60k m / h descendo uma inclinação de 10 % quando os freios em todas as quatro rodas travam. Se o coeficiente de atrito dinâmico entre os pneus e a estrada é 0,70 , encontre a
O cursor de 0,60k g desliza sobre a haste curva no plano vertical com atrito desprezível sob a ação de uma força constante F no fio guiado pelas pequenas polias em D . Se o cursor é liberado a partir