Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 95

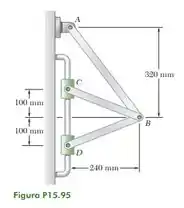
Dois colares C e D movem ao longo da barra vertical mostrada na figura. Sabendo que a velocidade do colar C é 660   m m / s para baixo, determine (a) a velocidade do colar D , (b) a velocidade angular na barra A B .

Passo 1

Bora pra questão 95 agora, meus caros (as)!

E já sabe, né! Nada melhor do que uma figura pra ajudar a entender uma questão.

Vamos fazer um esboço destacando vetorialmente as velocidades e o centro de rotação instantâneo desse sistema. Aqui está, nossa bela imagem...

Passo 2

a) Bom! Inicialmente, a gente tem que determinar a velocidade do colar D , que chamaremos de v D !

F e C fazem parte do centro de rotação instantâneo, na figura que desenhamos. E o enunciado nos dá o valor da velocidade v C do colar de 660   m m / s e para baixo...

v C = 660   m m / s   ↓

E para obter v D segundo a figura que esboçamos, temos que ele vai ser dado por...

v D = D F ω B D

Bom! A gente não sabe nem D F nem ω B D ! Portanto, vamos ter de obter os dois!

Vamos começar com D F , que é o mais acessível!

Por semelhança de triângulos, temos que...

320   m m 420   m m = 240   m m D F

D F = 420 ⋅ 240 320

D F = 315   m m

Passo 3

Agora vem a parte mais chatinha, que é obter ω B D !

Bom! A gente sabe que v C é de 660   m m / s para baixo. Em relação à barra B C , temos que temos que essa velocidade pode ser escrita como...

v C = ( C E ) ω B C

C E é fácil de obter! É só usar a semelhança de triângulos...

220   m m 320   m m = C E 240   m m

C E = 220 ⋅ 240 320

C E = 165   m m

Assim, isolando ω B C :

ω B C = v C C E

ω B C = 660   m m / s 165   m m

ω B C = 4   r a d / s   ⤿

Obtido ω B C , podemos descobrir a velocidade em B , v B , que será dada por...

v B = B E ω B C

E B E também vai ser de boas a gente obter!

Presta atenção! Pelo teorema de Pitágoras, temos que...

A B = 320   m m 2 + 240   m m 2

A B = 400   m m

Logo, novamente por semelhança de triângulos...

220   m m 320   m m = A E 400   m m

Só que...

A E = 400 - B E

Substituindo a relação acima, podemos obter B E ;

220   m m 320   m m = A E 400   m m

220   m m 320   m m = 400 - B E 400   m m

22 32 = 400 - B E 400

12800 - 32 ( B E ) = 8800

32 B E = 4000

B E = 4000 32

B E = 125   m m

E aí, v B será igual à...

v B = B E ω B C

v B = 125   m m ( 4   r a d / s )

v B = 500   m m / s

Passo 4

E é com esse v B   aí que a gente obteve que seremos capazes de determinar ω B D !

Analisando a barra B D , temos que...

v B = B F ω B D

E novamente, vamos obter B F por semelhança de triângulos! D F a gente sabe que vale 315   m m . Sendo assim, podemos estabelecer a seguinte relação...

240 315 = 400 400 + B F

96000 + 240 ( B F ) = 126000

240 B F = 30000

B F = 30000 240

B F = 125   m m

E com isso, isolando ω B D ...

ω B D = v B B F

ω B D = 500   m m / s 125   m m

ω B D = 4   r a d / s

Agora sim! Já podemos obter v D :

v D = D F ω B D

v D = 315   m m ( 4   r a d / s )

v D = 1260   m m / s   ↑

Passo 5

b) Pra finalizar, falta a velocidade angular na barra A B !

Bom! Pela imagem do P a s s o   1 , temos que...

v B = A B ω A B

E v B a gente já sabe o valor! A B também!

Logo, isolando ω A B e substituindo os valores numéricos...

ω A B = v B A B

ω A B = 500   m m / s 400   m m

ω A B = 1,250   r a d / s   ⤿

Pronto! Hasta la vista, baby!

Terminamos aqui!

Resposta

a)

v D = 1260   m m / s   ↑

b)

ω A B = 1,250   r a d / s   ⤿

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda desliza enquanto rola. Se v O = 1,2m / s e se a velocidade de A em relação a B é de 0,9 2m / s , localize o centro instantâneo C de velocidade nula e encontra a velocidade do ponto P.
O disco circular gira em torno de seu eixo z com uma velocidade angular ω = 2r a d /s . Um ponto P localizado sobre a borda possui uma velocidade dada por v = - 0,8 i - 0,6 jm / s . Determine as coord
A cuba oscilatória de produtos do Prob. 5/86 é apresentada aqui novamente. Se a manivela OB possui uma velocidade angular constante no sentido anti-horário de 0,944 rad/s, determine a velocidade angul
As duas polias estão presas uma na outra para formar um único conjunto rígido, e cada um dos dois cabos está enrolado firmemente em torno de sua respectiva polia. Se o ponto A no cabo de elevação poss
22. O disco está originalmente girando a ω 0 = 8 r a d s . Se ele é submetido a uma aceleração angular constante a = 6 r a d s 2 , determine as intensidades da velocidade e das compontes n e t da acel