Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 3
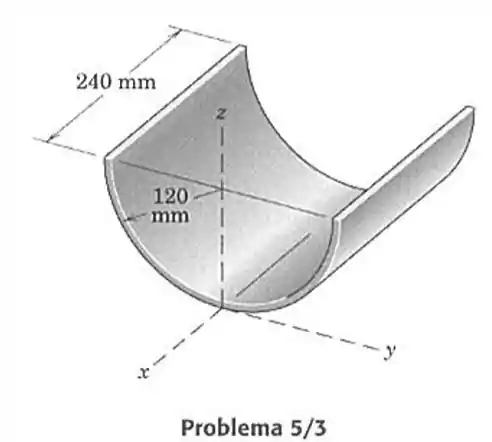
3- Especifique as coordenadas e do centro de massa da casca semicilíndrica
Passo 1
Pelo centroide do arco circular do exemplo 5/1 ( por que só existe a casca, diferente da área cheia do exercício 2), nós temos que:
Esse centroide está no eixo , que está presente no eixo mas começa no centro da semicircunferência.
Para , que pela semicircunferência.
Logo:
Para o raio igual a 120 mm.
Passo 2
Precisamos redesenhar a casca pra termos uma noção maior do que estamos fazendo.
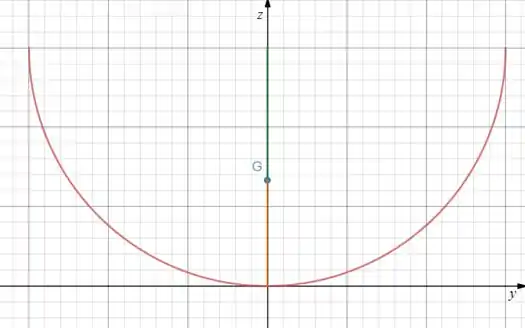
A reta verde é o tamanho de e a reta laranja seria o tamanho de , logo:
Passo 3
Como a casca está no eixo negativo de e se cortarmos ela no meio nós conseguiremos duas peças iguais, logo:
Resposta
Exercícios de Livros Relacionados
Coloque seu lápis sobre a posição da sua melhor estimativa visual do centroide da área triangular. Verifique a posição horizontal da sua estimativa referindo-se aos resultados do Exemplo 5/2.
4- Especifique as coordenadas x , y e z do centro de massa do quadrante do cilindro sólido homogêneo.
6- Determine as coordenadas do centroide da área sombreada:
5- Determine, por integração direta, a coordenada y do centroide da área sombreada.
9- Determine, por integração direta, as coordenadas do centroide da área trapezoidal.