Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 11
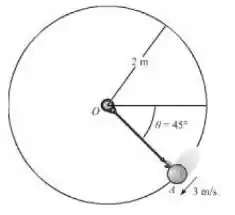
Se uma bola de 10 kg tem velocidade de 3 m/s quando está na posição A, ao longo da trajetória vertical, determine a tração na corda e o aumento na velocidade da bola nesta posição.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Como o carro está em uma trajetória circular, ele estará sujeito a uma força centrípeta. Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Passo 2
Vamos começar por esboçar o diagrama de corpo livre. Sendo assim, temos:
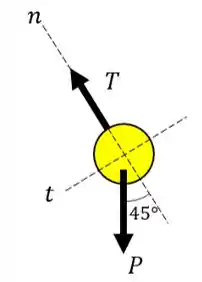
A bola está sujeita apenas a ação da tração da corda e da força peso. Como o peso possui uma componente na direção normal a trajetória da bola, a tração da corda deve ser suficientemente grande para contrabalancear esta componente e ser responsável pela força centrípeta na bola!
Passo 3
Vamos começar por determinar o valor da tração na corda. Para isto, vamos fazer um somatório de forças na direção normal. Portanto,
Passo 4
Agora podemos fazer o somatório de forças na direção tangencial para descobrir qual o valor da aceleração tangencial da bola. Isto é, qual é o aumento na velocidade da bola. Portanto,