Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 23
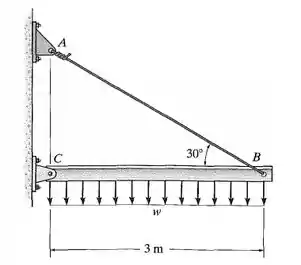
A viga é sustentada por um pino em e por um cabo de ancoragem de aço . Se o cabo tiver diâmetro de , determine quanto ele estica quando um carregamento distribuído agir sobre o tubo. O material permanece elástico.
Passo 1
Fala aí pessoal, bora para mais um exercício de resmat para tirar aquele notão na prova?
Ele quer o alongamento (a variação de comprimento) do cabo AB por causa desse carregamento distribuído em CB.
Como temos alongamento no cabo, a gente precisa descobrir a tensão nele, e assim a força normal nele. E por isso vamos fazer o diagrama de corpo livre (DCL) dessa estrutura. Aí depois vamos aplicar as equações da estática para achar a força em . O DCL fica:
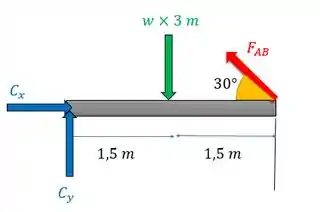
Essa força concentrada de no meio da barra BC é a força equivalente ao carregamento distribuído de ao longo dos da barra, tudo bem?
Passo 2
Aí vamos aplicar a equação de momento em para determinar a força , porque aí não precisamos nos importar com as forças em . Considerando o sentido horário como positivo:
Percebe que só a componente vertical de causa momento aqui. A componente horizonta aponta para , então ela não gera momento.
Substituindo o valor de e fazendo as continhas:
Passo 3
Com isso, vamos encontrar a tensão no cabo . Fica assim:
Como a área transversal é circular:
Substituindo:
Essa é a tensão atuante no cabo!
Passo 4
Agora que temos a tensão no cabo, precisamos do comprimento inicial do cabo para achar a deformação causada pela tensão.
Podemos tirar esse triângulo da nossa estrutura:
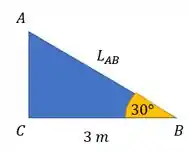
Aí podemos calcular o comprimento do cabo utilizando trigonometria, assim:
Passo 5
Como ele diz que o material permanece elástico, podemos usar a lei de Hooke para determinar a deformação do cabo de aço:
Substituindo os dados, lembrando que o valor tabelado para o módulo de elasticidade do aço-36 é :
Logo, pela deformação específica , podemos determinar o alongamento no cabo pela definição de deformação. Fica assim:
Substituindo os valores: