Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 81

O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, com resistência ao escoamento na tração de 300   M P a . Determinar o coeficiente de segurança, em relação ao escoamento, usando: (a) o critério da máxima tensão de cisalhamento; (b) o critério da máxima energia de distorção.

Passo 1

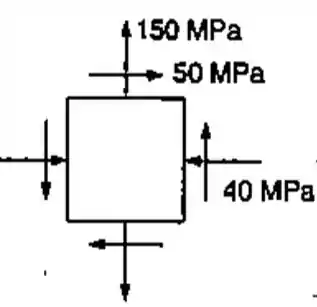
Para resolver essa questão a primeira coisa e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = - 40   M P a

σ y = 15 0   M P a

τ x y = 50   M P a

A partir daí vamos calcular o Raio do ciclo de mohr e a tensão média para se obter as tensões máximas e mínimas.

Passo 2

Vamos, também, achar a tensão média:

σ m é d = σ x + σ y 2

σ m é d = - 40 + 150 2

σ m é d = 55   M P a

Passo 3

Vamos achar o raio do ciclo de mohr fazendo:

R = σ x - σ y 2 2 + τ x y 2

R = - 40 - 150 ) 2 2 + 50 ²

R = 15050

R = 109,77   M P a

Passo 4

Agora vamos calcular as tensões normais máxima e mínima:

σ m á x = σ m é d + R

σ m á x = 5 5 + 109,77 = 164,77   M P a

σ m í n = σ m é d - R

σ m í n = 5 5 - 109,77 = - 54,77   M P a

Aplicando o critério da máxima tensão cisalhante da forma:

2 τ m á x = σ m á x - σ m í n

2 τ m á x = 164,77   - ( - 54,77 ) = 219,54     M P a

Observe que se o valor mínimo for maior do que zero utilizamos zero mesmo ao invés do valor achado.

O coeficiente de segurança é calculado como a tensão limite sobre a calculada:

C S = 300 219,54 = 1 , 36

Passo 5

Para letra B vamos utilizar o critério da máxima tensão de deformação, que se expressa da forma:

σ m á x 2 + σ m í n 2 - σ m á x ⋅ σ m í n

Neste critério vamos utilizar o σ m í n = 20,67   M P a .

164,77 2 + ( - 54,77 ) 2 - 164,77 ⋅ ( - 54,77 )   = 174,26   M P a

O coeficiente de segurança é calculado como a tensão limite sobre a calculada:

C S = 300 174,26 = 1,72

Resposta

a) C S = 1,36

b) C S = 1,72

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Devido à carga P, as componentes do estado plano de deformação no ponto do suporte são ϵ x = ( 500 × 10 - 6 ) , ϵ y = ( 350 × 10 - 6 ) e γ x y = ( - 430 × 10 - 6 ) . Use as equações de transformação d
6. As componentes do estado plano de deformação no ponto sobre uma chave são ϵ x = ( 120 × 10 - 6 ) , ϵ y = ( - 180 × 10 - 6 ) e γ x y = ( 150 × 10 - 6 ). Use as equações de transformação da deformaçã
7. As componentes do estado plano de deformação no ponto sobre o dente da engrenagem são ϵ x = ( 850 × 10 - 6 ) , ϵ y = ( 480 × 10 - 6 ) e γ x y = ( 650 × 10 - 6 ). Use as equações de transformação da
As componentes do estado plano de deformação no ponto sobre o dente da engrenagem são ϵ x = ( 520 × 10 - 6 ) , ϵ y = ( - 760 × 10 - 6 ) e γ x y = ( - 750 × 10 - 6 ). Use as equações de transformação d
As componentes do estado plano de deformação no ponto sobre a chave de porca são ϵ x = ( 260 × 10 - 6 ) , ϵ y = ( 320 × 10 - 6 ) e γ x y = ( 180 × 10 - 6 ). Use as equações de transformação da deforma