Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 7
7. As componentes do estado plano de deformação no ponto sobre o dente da engrenagem são , e ). Use as equações de transformação da deformação para determinar as deformações principais no plano e a deformação por cisalhamento máxima no plano e a deformação normal média. Em cada caso, especifique a orientação do elemento e mostre como as deformações distorcem o elemento no plano .
Passo 1
Primeiro, calcularemos as deformações principais no plano:
Trocando os valores numéricos na fórmula:
Passo 2
Agora, vamos calcular a tangente de no plano:
O primeiro ângulo , é dado pela metade de :
E para achar o outro ângulo , basta somar com :
Passo 3
Calculando também, :
Passo 4
E depois, calcularemos a deformação por cisalhamento máxima no plano, através da fórmula abaixo:
Trocando por valores numéricos adequados:
Passo 5
E a deformação normal média é dada por:
Substituindo os valores numéricos correspondentes:
Passo 6
O próximo passo é calcular a tangente de :
O primeiro ângulo é dado pela metade do ângulo :
E o segundo ângulo é dado por:
Resposta
As deformações principais no plano são:
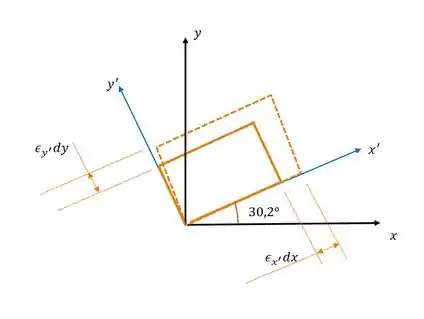
A deformação por cisalhamento máximo é:
E a deformação normal média é dada por:
