Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 62
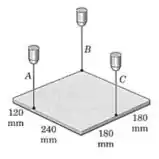
Uma chapa quadrada e uniforme de aço com de comprimento de aresta e uma massa de está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa em cada fio.
Passo 1
Vamos começar definindo os eixos , e e representando as forças envolvidas:
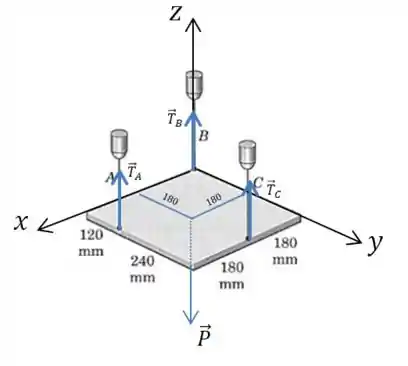
Se a placa está em equilíbrio nessa posição, os momentos totais em relação a cada eixo devem ser nulos.
Então precisamos encontrar expressões para cada um desses momentos.
Passo 2
Como todas as forças já são paralelas ao eixo , o momento resultante já é nulo:
Agora vamos dar uma olhada no momento em relação ao eixo . Temos que multiplicar cada força pela sua distância perpendicular até o eixo :
E o sinal negativo aparece no momento da força porque ela favorece a rotação no sentido contrário às outras forças.
Fazendo a mesma coisa para o momento em relação ao eixo encontramos o seguinte:
Agora vamos igualar todas essas expressões a zero, já que essa é a condição de equilíbrio:
Arrumando um pouco ficamos com um sistema de duas equações e duas variáveis desconhecidas:
Passo 3
Agora vamos resolver o sistema:
Uma forma de fazer isso é multiplicar a segunda linha por , e subtraí-la da primeira:
Onde , então:
E agora é só substituir esse valor em qualquer uma das equações para encontrar :
Passo 4
Ainda falta encontrar , mas para isso vamos precisar de outra equação de equilíbrio. Já analisamos o equilíbrio dos momentos, vamos ver agora o equilíbrio das forças:
Resposta
As forças são , e .