Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 146

Um excitador de massa excêntrica contrarotativo consiste de duas massas rotativas de 400 g que descrevem círculos de raio 150 mm com amesma velocidade, mas em sentidos opostos, e é colocado em um elemento de máquina para induzir uma vibração em regime permanentenesse elemento e para determinar algumas características dinâmicasdo elemento. A uma velocidade de 1.200 rpm, um estroboscópio mostra as massas excêntricas exatamente abaixo de seus respectivos eixosde rotação e o elemento passa a ter a sua posição de equilíbrio estático.Sabendo que a amplitude de movimento do elemento a essa velocidade é 15 mm e que a massa total do sistema é 140 kg, determine (a) aconstante de mola combinada k, (b) o fator de amortecimento c / c c . .

Passo 1

E ai gurizada tudo belezinha???

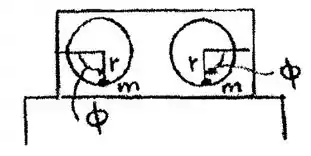
Freqüência de força: ω ƒ = 1 2 00   r p m = 125.664     r a d / s

Desequilibriu de uma massa: m = 400   g = 0.4   K g

r = 150   m m = 0.15   m

Força de agitação: P = 2   m r ω ƒ 2 sin ⁡ ω ƒ t

= 2 0.4 0.15 125.664 2 sin ⁡ ω ƒ t

= 1.89497 × 10 3   sin ⁡ ω ƒ t

P m = 1.89497 × 10 3   N

Massa total: M = 140   K g

Por equação, a resposta vibratória do sistema é, x = x m sin ⁡ ω ƒ t - φ

Onde x m = P m k - M ω ƒ 2 + ( c ω ƒ ) ²

E tan ⁡ φ = c ω ƒ k - M ω ƒ 2

Desde a φ = 90 ° = π 2 , tan ⁡ φ = ∞             e             k - M ω ƒ 2

(a)Costant de mola combinada:

= 140 125.664 2 = 2.2108 × 10 6 N

A amplitude observada é, x m = 15   m m = 0.015   m

A partir de c = 1 ω ƒ P m x m 2 - k - M ω ƒ 2 = P m ω ƒ x m

= 1.89497 × 10 3 ( 125.664 ) ( 0.015 ) = 1.00531 × 10 3   N ∙ s / m

Coeficiente de amortecimento critico: c c = 2 k M

= 2 ( 2.2108 × 10 6 ) ( 140 ) = 35.186 × 10 3   N ∙ s / m

Passo 2

(b)Fator de amortecimento: c c c = 1.00531 × 10 3 35.186 × 10 3

Resposta

a) k = 2.21   M n / m

b) c c c = 0.0286

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19.111. Um pêndulo simples de comprimento l é suspenso de um cursor C que é forçado a mover-se horizontalmente de acordo com a relação x C = δ m sin ⁡ ω f t . Determine o intervalo de valores de f par
19.112. Um peso de 1,2 kg de um pêndulo simples de comprimento l 600 mm é suspenso de um cursor C de 1,4 kg. O cursor que é forçado a mover- -se horizontalmente de acordo com a relação xC m sen f t, c
Solucione o Problema, considerando que o coeficiente de amortecimento do amortecedor é de c 300 N s/m.
No caso da vibração forçada de um sistema, determine o intervalo devalores do fator de amortecimento c / c c , para o qual o fator de ampliação sempre diminuirá quando a razão de frequência ω ƒ / ω n
Uma barra uniforme de massa m é suportada por um pino em A e uma mola de constante k em B e está ligada em D a um amortecedor de coeficiente de amortecimento c. Determine, em termos de m, k e c, para