Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 58
Expresse cada uma das três forças que atuam sobre o suporte na forma vetorial cartesiana com relação aos eixos e . Determine a intensidade e direção de de modo que a força resultante seja direcionada ao longo do eixo positivo e tenha uma intensidade .
Passo 1
Fala, querido! Ele quer que a gente expresse nossas forças na forma vetorial e ache e sua orientação.
Vamos fazer a primeira parte que o exercício nos pede, expressar as forças de forma cartesiana com relação aos eixos, como ainda não temos as respostas de ela ficará assim por enquanto:
Repara que aponta para o sentido positivo dos dois eixos e o ângulo da sua orientação é oposto a y. Então o seno fica na componente y e ambas ficam positivas.
Temos que está no sentido positivo de x. E ela está na direção positiva de x. Logo, nesse eixo ela vale o valor do seu próprio módulo e em ela vale zero:
Já para , a situação é que ela está no eixo y, então x vai zerar e y fica sendo o próprio valor da força. Como ela aponta para baixo, ela fica negativa:
Feito. Agora vamos achar e !
Passo 2
Agora vamos encontrar a . Dada a direcionada ao longo do eixo (a de x no anti-horário). Antes, vamos decompor a .
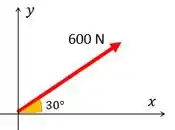
Como o ângulo tá colado em x, nessa componente fica o cosseno e na outra o seno. Ambas postivas.
Passo 3
Sabemos que:
Então vamos somar as forças em seus devidos eixos.
Para :
Para
E nosso vetor cartesiano de fica:
Passo 4
Assim, podemos encontrar o ângulo da dividindo as duas equações:
E então podemos achar nossa :