Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 101
Expresse a força como um vetor em termos dos vetores unitários , e . Determine os ângulos , e que faz com os eixos positivos , e .
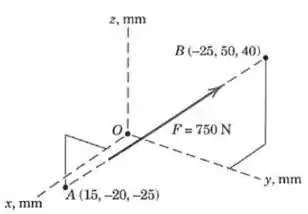
Passo 1
Vamos começar escrevendo a força em forma vetorial. Começamos encontrando um vetor que liga os pontos e :
Queremos encontrar o vetor unitário na direção de , então precisamos calcular o seu módulo:
Agora é só dividir pelo seu módulo para encontrar o vetor unitário :
Passo 2
Agora podemos escrever a força em forma vetorial:
Passo 3
Agora vamos usar a seguinte fórmula para encontrar o ângulo que a força faz com cada eixo:
(Se não quiser decorar, você pode demonstrar essa fórmula usando a definição de produto escalar!)
Aplicando essa fórmula em cada uma das componentes:
E agora é só calcular os cossenos usando a calculadora:
Resposta
A força resultante é e os ângulos são , e .