Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 103
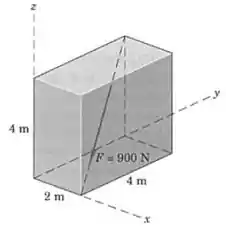
A força tem um módulo de e atua ao longo da diagonal do paralelepípedo, como mostrado. Expresse em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus componentes , e .
Passo 1
Queremos expressar como um módulo multiplicado por um vetor unitário, então precisamos começar calculando esse vetor.
Uma forma interessante de escrever esse vetor é pensar nele como o que liga dois pontos e :
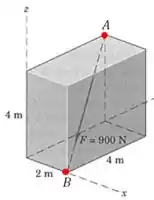
Agora vamos encontrar o vetor unitário nessa direção:
Passo 2
E a força tem módulo e aponta na direção de , então:
E agora fica fácil calcular as componentes:
Resposta
A força é dada por e as componentes são , e .
Exercícios de Livros Relacionados
O mastro rígido com barras cruzadas é suportado pelos três cabos mostrados. Um tensionador em D é apertado até induzir uma força trativa T de 1,2k N em C D . Expresse T → como um vetor. Faz alguma dif
Use o resultado dado para o problema 2 / 105 e determine o módulo T G F da projeção de T → sobre a linha G F .Imagem do problema 2 / 105 :
O tensionador é apertado até que a força trativa no cabo A B valha 2,4k N . Determine a expressão vetorial para a força trativa T → , como uma força atuando no elemento A D . Ache também o módulo da p
O cabo B C suporta uma força trativa de 750N . Escreva esta força trativa como uma força T → atuando no ponto B em termos dos vetores unitários i , j e k . O cotovelo em A forma um ângulo reto.
Desenvolva uma expressão para a projeção F D C da força F → sobre a linha direcionada de D a C .