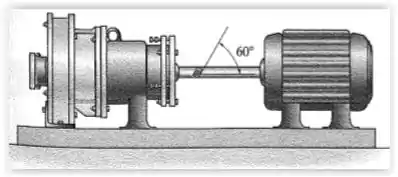
12. Um extensômetro está montado no eixo de aço de de diâmetro como mostra a figura. Quando o eixo está girando a uma velocidade angular e usando um anel corrediço, a leitura no extensômetro é . Determine a potência de saída do motor. Considere que o eixo está sujeito somente a um torque.

Considerando que no estado inicial, não há nenhuma componente de estado plano de deformação, temos que:

Em seguida, vamos calcular a deformação por cisalhamento de um elemento orientado pelo ângulo , conforme mostra a figura, por meio da fórmula de transformação da deformação no eixo :

Mas a própria questão nos diz, né, que a leitura do extensômetro no eixo, que vai ser a nossa direção , vale . Logo, encontramos o valor de . Vamos então, substituir os valores numéricos pertencentes a cada variável da nossa equação:

Como foi dado que o aço é do tipo , temos que:

Então, utilizaremos a fórmula de tensão de cisalhamento:

E substituímos os valores numéricos de cada variável:

Encontrada a tensão de cisalhamento, vamos utilizar então a seguinte fórmula, que todo mundo já tá careca de saber, para encontrar o nosso torque .

Trocando as variáveis pelos seus respectivos números, chegamos à:

Por fim, calcularemos a potência necessária, pela equação abaixo ( o produto do torque pela velocidade angular). Você pode tá achando essa expressão estranha, mas o produto das grandezas dimensionais dela, resulta em , que tem dimensão de potência. Então, estamos corretos!