Para o instante representado, o carro tem uma velocidade de , que está aumentando na taxa de cada segundo. Simultaneamente, o carro também tem uma velocidade de enquanto contorna a curva e está reduzindo a velocidade na taxa de cada segundo. Determine a aceleração que o carro aparenta ter para um observador no carro .

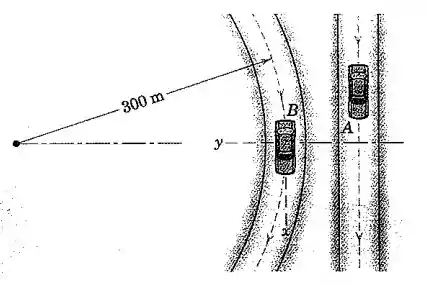
Conforme as direções e representadas na figura, e lembrando que , a aceleração do carro pode ser escrita assim:

Já o carro tem duas acelerações, a normal e a tangencial. A aceleração tangencial ocorre no sentido negativo do eixo , pois o carro está diminuindo sua velocidade:

A aceleração normal de aponta para o centro do círculo, ou seja, para o sentido positivo do eixo , e então: