O guia vertical é liso, e o anel de 5 kg é solto do repouso em A. Determine a velocidade do anel quando ele está na posição C. A mola tem um comprimento não deformado de 300 mm.
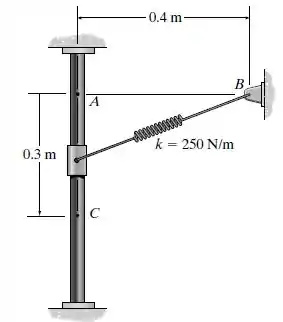
Passo 1
Com referência definida na figura representativa, a energia potencial gravitacional do bloco nas posições (A) e (C) podem ser escritas através de:
O outro tipo de energia associada ao problema é a fornecida pela mola, isto é, potencial elástica, definida por:
Analisando os pontos definidos pelo diagrama:
Ponto A: Origem do sistema.
- Pela referência definida, tem-se que a consequência imediata será =0.
- Nesta posição, através do triângulo retângulo, pode-se averiguar que a deformação inicial da mola é dada pelas posições inicial e final dos estados, dessa forma:
Ponto B: Posição de análise.
- A partir da referência, obtém-se que , por estar abaixo da origem definida.
- Nesta posição, é necessária uma análise a partir do triângulo retângulo formado em relação ao segmento CB, de modo que a deformação será dada pelo comprimento do segmento CB subtraída a distância vertical percorrida, portanto:
Passo 2
Identificadas as energias atuantes no sistema, admitindo que sejam conservativas, a lei de conservação da energia mecânica será:
Substituindo as expressões no balanço energético, tem-se que:
Passo 3
Com as conclusões acerca dos pontos inicial e final da análise, a expressão de conservação de energia será:
Resposta
A velocidade do anel para quando a posição C for alcançada será de 2,094 m/s.