Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 196
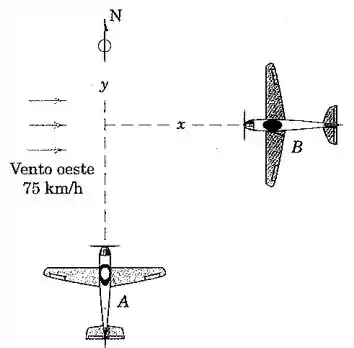
O pequeno avião inicialmente voando para o norte com uma velocidade em relação ao solo de encontra um vento oeste de (soprando para o leste). O avião voando para o oeste com uma velocidade em relação ao ar de passa quase na mesma altitude. Determine o módulo e a direção da velocidade que aparenta ter para o piloto de .
Passo 1
Quando o avião encontra o vento, ele também adquire essa velocidade para a direita em relação ao solo. Escrevendo isso vetorialmente:
Da mesma forma, o avião também sofrerá esse efeito, mas lembre-se que ele já estava voando na direção do vento, em sentido contrário:
Assim, já podemos calcular a velocidade relativa do avião em relação ao avião :
Passo 2
Show! Agora calculamos o módulo dessa velocidade relativa assim:
Lembre-se que o ângulo com o eixo é calculado assim:
Ou seja, o vetor aponta para acima do leste.
Resposta
acima do leste