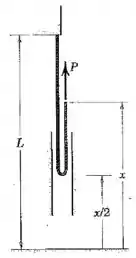
A extremidade livre da corda flexível e inextensível de massa por unidade de comprimento e o comprimento total recebe uma velocidade constante para cima . Escreva expressões para , para a força que suporta a extremidade fixa, e para a tração na corda na curva em termos de . (Para a curva de tamanho desprezível, a tração é a mesma em ambos os lados).

Agora podemos usar a equação de trabalho energia na forma diferencial, considerando que a força é que gera deslocamento no sistema ao longo da coordenada :

E para a energia cinética temos simplesmente que considerar a massa e a velocidade da parte em movimento:

Ou seja:

E então:

Beleza, já temos a força , agora vamos procurar . Vamos usar a expressão que dá a resultante das forças externas:

Onde é a quantidade de movimento da corda na direção de . Nesse caso temos a força que suporta a extremidade física, a força conforme o desenho e o peso da corda:

E agora vamos escrever uma expressão para :

Já que é a massa da porção da corda que está do lado que tem movimento. Tirando a derivada temporal dessa grandeza:

Já que a velocidade é constante () e .

Então ficamos com:

Substituindo com a expressão que encontramos para :

Agora falta encontrar a tração na corda na curva. Como disse o enunciado, podemos considerar que a tração é a mesma em ambos os lados, isso quer dizer que podemos calcular isso olhando para algum outro trecho da corda, e a tração será a mesma.

Olhando para a parte fixa da corda (esquerda), a soma das forças tem que se anular, já que ela está em equilíbrio, então:

E é a tração exercida pelo outro pedaço da corda.

Resolvido!