Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 23

As três pequenas esferas, cada uma com massa m , estão presas às hastes leves de modo a formar uma unidade rígida apoiada no plano vertical pela superfície circular lisa. A força de módulo constante P é aplicada perpendicular a uma haste em seu ponto médio. Se o conjunto parte do repouso em θ = 0 , determine

(a) a força mínima P m í n que levará o conjunto ao repouso em θ = 60 ° e

(b) a velocidade em comum v das esferas 1 e 2 quando θ = 60 ° se P = 2 P m í n .

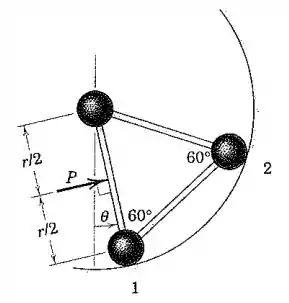
Passo 1

(a) Como a força P realiza trabalho sobre o sistema, temos:

U P = Δ T + Δ V g

Porém, estamos considerando um sistema que parte do repouso em θ = 0 e retorna ao repouso em θ = 60 ° . Logo, Δ T = 0 :

U P = Δ V g

Para calcularmos o trabalho U P da força P m í n , perceba que ocorreu um deslocamento angular de θ = 60 ° = π / 3 , então:

U P = P m í n r 2 π 3

U P = π 6 r P m í n

Passo 2

Para calcular a variação Δ V g de energia potencial gravitacional, observe como vai ficar a configuração das esferas em θ = 60 ° :

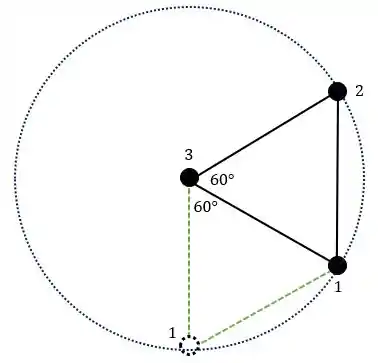
Como as hastes formam um triângulo equilátero, com um dos vértices no centro, a esfera 1 passa a ocupar o lugar inicial da esfera 2 , a esfera 2 sobe verticalmente uma altura r , e a esfera 3 não se move.

Então, sendo h 1 , h 2 e h 3 as alturas iniciais das esferas 1 , 2 e 3 , temos:

Δ V g = Δ V 1 + Δ V 2 + Δ V 3

Δ V g = m g h 2 - h 1 + m g h 2 + r - h 2 + m g h 3 - h 3

Δ V g = m g r + h 2 - h 1

Porém, perceba que o comprimento h 2 - h 1 equivale à metade do comprimento da haste:

Δ V g = m g r + r 2

Δ V g = 3 2 m g r

Logo, utilizando U P = Δ V g , obtemos:

π 6 r P m í n = 3 2 m g r

P m í n = 9 π m g

Passo 3

(b) Se para o equilíbrio, tínhamos U P = π 6 r P m í n , então o novo trabalho da força P = 2 P m í n será:

U P ' = π 6 r 2 P m í n

U P ' = π 6 r 2 9 π m g

U P ' = 3 m g r

Como θ = 60 ° novamente, teremos a mesma configuração espacial das esferas, e portanto:

Δ V g ' = Δ V g

Δ V g ' = 3 2 m g r

Mas agora teremos variação de energia cinética devida à velocidade final v das esferas 1 e 2 , dada por:

Δ T ' = 2 1 2 m v 2 - 0

Δ T ' = m v 2

Utilizando, U P ' = Δ T ' + Δ V g ' , obtemos:

3 m g r = m v 2 + 3 2 m g r

v = 3 2 g r

Resposta

(a) P m í n = 9 π m g

(b) v = 3 2 g r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro hastes esbeltas idênticas, cada uma de massa m, são soldadas em suas extremidades para formar um quadrado, e os vértices são em seguida soldados a um aro leve de metal com raio r . Se o conjunt
O aro circular leve de raio r carrega uma tira uniforme pesada de massa m em torno da metade de sua circunferência e é liberado a partir do repouso sobre a inclinação na posição superior mostrada. Apó
Um telescópio espacial é apresentado na figura, um dos volantes de reação de seu sistema de controle de orientação angular está girando a 10r a d / s conforme indicado, e nessa velocidade o atrito no
O regulador mecânico de esferas opera com um eixo vertical O - O . Quando a velocidade no eixo N é aumentada, o raio de rotação das duas esferas de 1,5 kg tende a aumentar, e a massa A de 0 kg é eleva
Em uma atração acrobática, um homem de massa m A pula de uma plataforma elevada sobre a extremidade da viga leve, porem resistente, com uma velocidade v 0 . O menino de massa m B é lançado para cima c