Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 71
A figura mostra uma plataforma inclinável de caminhão para descarregar contêineres carregados. O contêiner carregado de pode ser considerado como um bloco retangular homogêneo maciço com centro de massa em . Se a roda de apoio é impedida de se movimentar, calcule a força exercida pela plataforma sobre a roda de apoio , quando o caminhão parte do repouso com uma aceleração para frente de . Despreze o atrito em .
Passo 1
Vamos começar calculando o momento resultante em relação ao ponto :
E as únicas forças que produzem momento em relação a esse ponto são as componentes da força peso e a força :
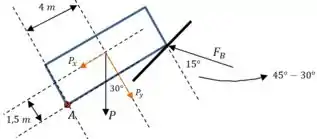
E então precisamos calcular e para resolver o problema.
Passo 2
Começamos por , o momento de inércie do contêiner em relação ao ponto :
E vamos usar algumas relações geométricas para calcular , que é na verdade a aceleração angular associado ao ângulo que, no instante retratado no desenho, mede :
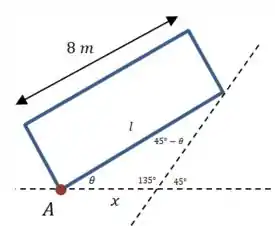
Podemos usar a lei dos senos para escrever uma relação entre as grandezas da figura:
A segunda derivada de será igual à aceleração do centro de massa do contêiner, e a segunda derivada de será igual à aceleração angular.
Derivando uma vez em relação ao tempo:
E derivando mais uma vez:
No instante em que o caminho parte do repouso com uma aceleração , podemos supor que a velocidade angular do contêiner é muito pequena, e portanto é desprezível:
E agora é só calcular no caso em que , e :
Onde o sinal negativo indica que a aceleração angular é no sentido anti-horário, que nós tomamos como positivo no cálculo do momento.
Passo 3
Agora vamos substituir esses valores na expressão que encontramos no primeiro passo:
Resposta
A força exercida pela plataforma é .