A viga I de tem uma massa de e é mantida na posição horizontal pelo pino em e pelo cabo vertical que passa em torno da polia em e em torno do tambor do guincho motorizado de em . Se o motor do guincho produz um torque de partida de , calcule a força vertical inicial suportada pelo pino em . Considere a viga como uma barra esbelta e o conjunto do guincho como uma massa concentrada no centro da polia. (A componente horizontal da força sobre o pino é nula?)
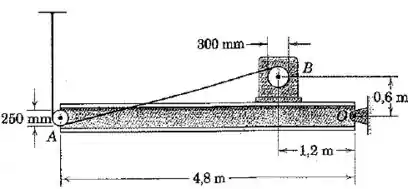
Passo 1
Vamos começar calculando o momento de inércia do sistema em relação ao ponto :
E a tensão fornecida à corda pelo momento de aplicado pelo motor pode ser calculado em função do raio do tambor em :
Passo 2
Com esses resultados, podemos calcular a aceleração angular do sistema:

E então:
Passo 3
Agora podemos usar a segunda lei de Newton para encontrar a força (força vertical suportada pelo pino):
Onde é a massa da viga e é a posição do seu centro de massa em relação ao pino.
Conforme o desenho, as forças que agem na direção vertical são os dois pesos, a força que queremos calcular, e a tração :
Então:
Resposta
A força vertical inicial suportada pelo pino é .