Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 51
Na figura é mostrado um pequeno elevador industrial com um pé de liberação. Existem quatro molas idênticas, duas de cada lado do eixo central. A rigidez de cada par de molas é de 2k. Ao projetar a elevação, especifique o valor de k que garantirá um equilíbrio estável quando a elevação suportar uma carga (peso) L na posição onde θ = 0 sem força P no pedal. As molas são igualmente pré-comprimidas inicialmente e pode-se presumir que atuam sempre na direção horizontal.
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa
Como somos obrigados a determinar k, que garantirá a estabilidade sem nenhuma força atuando no pedal, podemos desprezar a força P, também podemos desprezar os pesos, uma vez que não temos informações sobre ela. Sabendo disso, podemos escrever a equação de equilíbrio como
(1)
Podemos ver no esboço que as distâncias x e y são
Embora a mudança no comprimento das molas A e B sejam
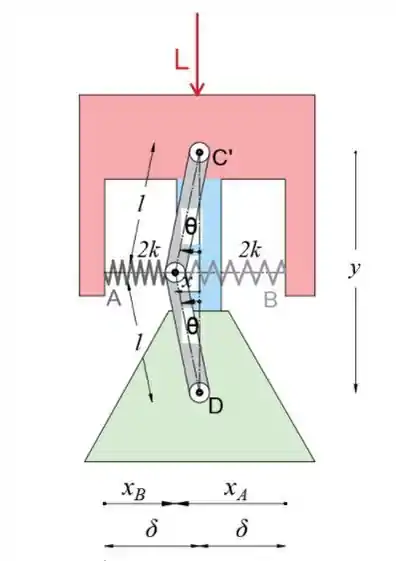
Passo 2
Trabalho virtual feito pela força F
Substituiremos
Derivamos ambos lados da equação
(2)
Uma vez que temos dois pares de molas presas ao sistema, ambos com rigidez 2k, podemos escrever a expressão para energia potencial elástica como
Substituiremos XA e XB por , respectivamente
Derivaremos ambos lados da equação
(3)
Passo 3
A seguir, substituiremos δUL e δVe pelas expressões (2) e (3) na equação de equilíbrio (1)
Podemos dividir ambos os lados da equação por 2lδθ
Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero
Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ em (4)
(4)
Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ em (4)
A partir daqui, podemos expressar a rigidez da mola k como