Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 92
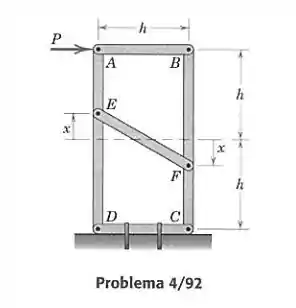
A figura representa a estrutura de uma unidade de armazenamento em prateleiras, onde as prateleiras intermediárias não estão mostradas. A variável representa diferentes configurações de fixação. Determine, e faça um gráfico na faixa , a força no suporte , devida à força aplicada . O que acontece se ?
Passo 1
Vamos aqui primeiro isolar as barras laterais e , e tentar fazer as equações de equilíbrio para elas para tentar determinar . Temos muitas forças desconhecidas na parte de baixo, nos pontos e , mas conseguiremos evitar essas forças fazendo as equações de momento nesses pontos (2 incógnitas, e , e duas equações, momento em e momento em ). Vamos desenhar os diagramas de corpo livre, nos atentando a colocar os sentidos contrários para as mesmas forças em cada lado:
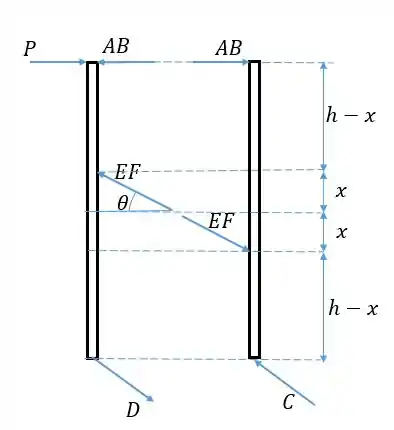
Passo 2
Vamos primeiro fazer na barra da esquerda o momento em torno de . Precisamos primeiro do cosseno do ângulo para obter a componente horizontal da força . Temos:
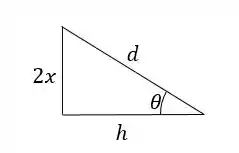
Agora vamos fazer o momento em torno de :
Isolamos para substituirmos depois:
Passo 3
Agora, para a barra da direita, fazemos o momento em relação a :
Substituimos agora :
Vamos passar para o outro lado e colocar em evidência:
Agora substituímos o valor de encontrado no passo 2:
O sinal negativo indica que a força no elemento é de tração e não de compressão como mostramos.
Passo 4
Agora representamos em função de em um gráfico.
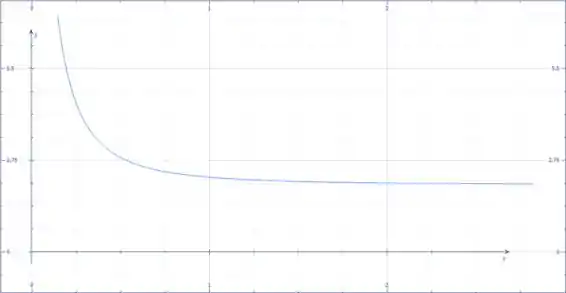
Se , temos uma ideterminação. A estrutura colapsa para essa configuração, que tem a barra horizontal.
Resposta
Para temos um colapso da estrutura.