Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 130
Resolva o Problema 13.129, considerando que a força de frenagem constante de 20 kN é aplicada no carro B mas que os freios no carro A não são aplicados.
Passo 1
Essa é uma questão interessante envolvendo o princípio de impulso e quantidade de movimento linear. Agora a força de frenagem é aplicada somente no vagão B. Para determinar o tempo necessário para o trem para, temos que considerar a massa dos dois vagões. Primeiro, vamos esquematizar isso no diagrama de corpo livre:
Somando os vetores na direção x, com sentido positivo para a esquerda, temos que:
Passo 2
Substituindo os valores de massa, velocidade e força de frenagem na equação do passo 1, temos:
O tempo total de frenagem é 30,14 s
Passo 3
Agora, para calcular força do engate entre os vagões durante a desaceleração, vamos analisar somente a desaceleração no vagão A. Vamos representar isso em um diagrama de corpo livre:
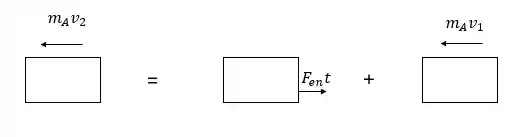
A força do engate é contrária ao movimento, porque ao desacelerar o engate exerce uma força sobre o vagão B, ou seja, uma força “saindo” de A. Assim, relacionando os vetores mostrados no diagrama de corpo livre, temos:
A força no engate é de 11,62 kN.
Resposta
- 30,14 s
- 11,62 kN