Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 121

Um fio tem peso de 2   N / m . Se ele pode ser esticado por 10 m e possui uma flecha de 1,2 m, determine o comprimento do fio. As extremidades do fio são apoiadas a partir da mesma elevação.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Esta é uma questão semelhante ao exercício resolvido 7.13. Pelo menos em termo de geometria (e solução de equação), ela é idêntica. Relembrando, a geometria é:

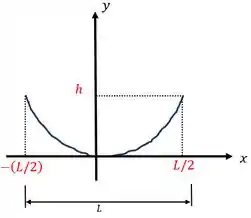
Aqui temos um fio de peso uniforme w 0 = 2   N / m . Sabemos que o fio pode ser esticado por um comprimento L = 10   m e assim possuir uma flecha y = h = 1,2   m .

Com posse de todas essas informações, precisamos determinar o comprimento total do fio.

Bom, como a resolução das equações desta questão é exatamente as mesmas do Exemplo 7.13, vamos utilizar equações já desenvolvidas.

Sendo assim, vamos as contas!

Passo 2

A primeira equação que vamos utilizar é a que utilizamos para obter a flecha do fio, a equação y = f x . Do Exemplo 7.13 nós temos que:

y = F H w 0 cosh ⁡ w 0 F H x - 1

Desta equação nós temos todas as informações, com exceção de F H , que será de extrema importância para obtermos o comprimento total do cabo!

Sendo assim, vamos substituir todos os valores que a questão nos deu. Desta forma, temos:

1,2 = F H 2 cosh ⁡ 2 F H ⋅ 5 - 1

Vamos utilizar ela para obter que F H = 21,2   N .

Passo 3

Agora que obtivemos F H , vamos obter a metade do comprimento do fio. Para isto, temos a relação s = f x , dada por:

s = F H w 0 senh ⁡ w 0 F H x

Relembrando, a variável s começa a medir a partir da origem. Portanto, se queremos o comprimento do fio de uma ponta a outra, realmente temos que multiplicar o valor de s por 2.

Sendo assim, vamos obter o valor de s até uma extremidade do fio. Logo,

s = 21,2 2 senh ⁡ 2 21,2 5

s = 5,18   m

E o comprimento total será:

s t o t a l = 2 s = 10,36   m

E assim finalizamos a questão!

Resposta

s t o t a l = 10,36   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo se romperá quando a tração máxima alcançar T m á x = 10k N á . Determine a flecha mínima h se ele suporta a carga distribuída uniforme de w = 600N / m .
A corrente de 80 m de extensão é fixada em suas extremidades e içada em seu ponto intermediário B por um guindaste. Se a corrente tem peso de 0,5k N / m , determine a altura mínima h do gancho a fim d
A viga de elevação é usada para o manuseio de materiais. Se a carga suspensa tem peso de 2k N e centro de gravidade em G , determine a posição d dos suportes no topo da viga, de modo que não haja mome
A viga A B falhará se o momento fletor máximo em D atingir 800N ∙ m ou a força normal no membro B C se tornar 1500N . Determine a maior carga w que ela pode suportar.
O cabo de 10k g / m é suspenso entre os suportes A e B. Se o cabo pode sustentar uma tração máxima de 1,5 kN e a fecha máxima é 3 m, determine a distância máxima L entre os suportes.