Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 47
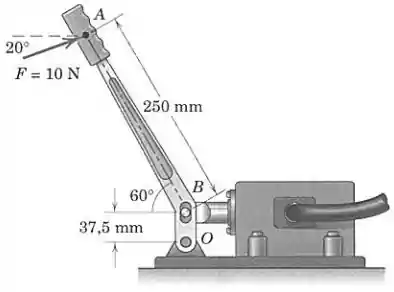
A força de é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto .
Passo 1
Pessoal, a força pode ser decomposta numa força horizontal e numa força vertical , de modo que:
Passo 2
Como o ponto de aplicação da força é , essas duas componentes produzem momento em relação a no sentido horário (negativo), e então:
Resposta
(sentido horário)
Exercícios de Livros Relacionados
3.15. Desenvolva os produtos vetoriais B × C e B ' × C , onde B = B ' , e use os resultados obtidos para demonstrar a identidade: sin α cos β = 1 2 sin α + β + 1 2 sin α - β
3.14. Um mecânico utiliza um pedaço de tubo AB como alavanca para esticar a correia de um alternador. Quando ele empurra a alavanca para baixa em A, uma força de 485N é exercida sobre o alternador em
3.13. A porta traseira de um carro é sustentada por uma haste hidráulica BC. Se a haste exerce uma força de 566N dirigida ao longo de sua linha de centro sobre a rótula em B, determine o momento da fo
3.11. Sabe-se que é necessária uma força com um momento de 960N ⋅ m em relação a D para endireitar o mourão CD. Se a capacidade do guincho AB 2400N , determine o valor mínimo da distância d para se cr
A cancela de travessia da linha férrea consiste em um braço de 100 kg com um centro de massa em Ga e o contrapeso de 250 kg com um centro de massa em GW. Determine a intensidade e o sentido direcional