Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 40
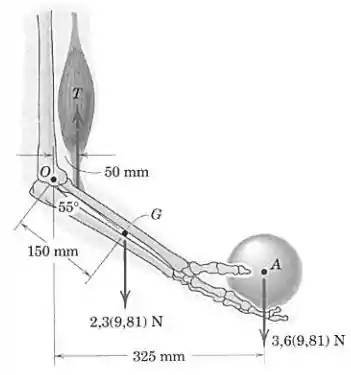
Elementos do braço são mostrados na figura. A massa do antebraço é de , com centro de massa em . Determine o momento combinado em relação ao cotovelo em dos pesos do antebraço e da esfera homogênea de . Qual deve ser a força trativa no bíceps, de modo que o momento total em relação a seja zero?
Passo 1
Pessoal, o momento em relação a vai ser a soma dos momentos das forças em e em :
As duas forças são verticais e têm momentos no sentido horário (negativo). Já sabemos que a distância horizontal de até é , então:
Passo 2
Além disso, a distância real de até é , então a distância horizontal será , e portanto:
Desse modo, podemos somar os dois momentos calculados para obter:
Passo 3
Se quisermos que o momento total em torno de seja nulo, precisamos de uma força com momento no sentido anti-horário, para anular o efeito das demais forças. Essa força será a tração para cima, que age a uma distância horizontal de , conforme a figura do enunciado.
Então:
Resposta
(sentido horário)