Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 41
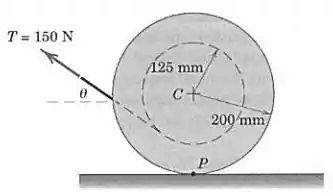
Um puxão de é dado em uma corda, que está firmemente enrolada na parte interna do tambor. Determine o momento de em relação ao centro do tambor em . Em que ângulo , deve ser aplicado de modo que o momento em torno do ponto de contato seja zero?
Passo 1
Galera, vamos considerar que o raio interno do tambor é , e o raio externo é . Então, o momento da força em relação ao centro será no sentido horário (negativo) e dado por:
Passo 2
Para que o momento em torno do ponto de contato seja zero, a linha de ação da força deve passar por , como mostra a figura a seguir:
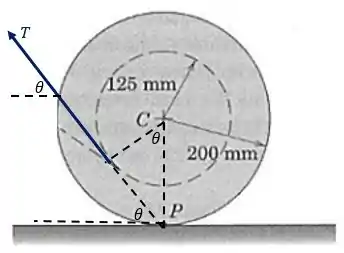
De acordo com a geometria da figura, o ângulo pode ser calculado pelas dimensões do triângulo retângulo pontilhado:
Resposta
(sentido horário)
Exercícios de Livros Relacionados
Uma força P de 49 N é aplicada em uma alavanca de câmbio. O momento P sobre B é horário e tem a intensidade de 28N ⋅ m . Determine o valor de α .
Uma válvula de pedal para um sistema pneumático é articulada em B. Sabendo que α = 28 º º, determine o momento de uma força de 16 N em relação ao ponto B decompondo a força em componentes ao longo de
Uma força P de 35N é aplicada em uma alavanca de câmbio. Determine o momento de P sobre B quando α é igual a 25 º º.
Um guincho AB é usado para endireitar um mourão. Sabendo que a tração no cabo BC é 1140N e o comprimento d é 1,9 m, determine o momento em relação a D da força exercida pelo cabo em C decompondo tal f
Para uma alavanca de câmbio mostrada na figura determine a intensidade e direção da menor força P que gera um momento no sentido horário de 24N ⋅ m sobre B.