Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 16
A talha portátil de carro é operada pelo sistema hidráulico cilindro que controla a horizontal
movimento da extremidade A do elo na ranhura horizontal. Determine a compressão C no pistão haste do cilindro para suportar a carga P em um altura h.
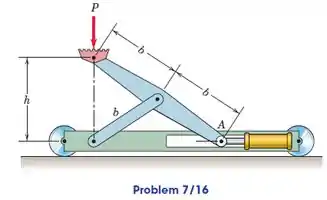
Fonte: Meriam - Estática - 7ª ed
Passo 1
Fala aí!
Bora pra mais uma!
Primeiro, o problema nos dá que há uma talha portátil de carro, conforme a figura. Observemos que há uma compressão de uma carga P que gera deslocamento no eixo vertical, representado por h.
Em segunda análise, o problema também nos informa que há uma força de compressão C dentro do cilindro que gera um deslocamento horizontal, que podemos representar por x. Devemos determinar qual a intensidade da compressão C.
Passo 2
Dito isso, podemos inferir, de acordo com o princípio do trabalho virtual que:
Por geometria, podemos encontrar que h:
E derivando, temos:
E o deslocamento x:
E derivando, temos:
Passo 3
Assim, aplicando os termos na equação 1:
Rearranjando valores, temos:
Porém, pela geometria do problema podemos descobrir quem é a cotangente de :
Assim:
Resposta
Portanto