Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 130
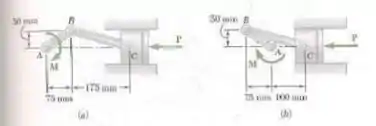
Uma força de intensidade é aplicada no pistão do motor mostrado na figura. Para cada uma das duas posições mostradas, determine o binário necessário para manter o sistema em equilíbrio.
Passo 1
Temos o valor da força e desejamos encontrar o valor do momento de binário de tal forma que nosso sistema permaneça em equilíbrio, ou seja, as forças em todas as direções devem ser nulas. Primeiramente observemos o ângulo cujo qual podemos encontrar o valor da tangente
Analisando, agora, as condições de equilíbrio vamos ter
Adotando o sentido anti-horário como positivo vamos ter
Passo 2
Já para o segundo caso vamos ter a seguinte avaliação
Assim, aplicando as condições de equilíbrio vamos obter
Adotando o sentido anti-horário como positivo vamos ter
Resposta
Exercícios de Livros Relacionados
O homem usa o carrinho de mão para subir o material pelo degrau. Se o carrinho e seu conteúdo possuem massa de 50 kg com centro de gravidade em G , determine a reação normal nas duas rodas e a intensi
O conjunto da plataforma tem peso de 1000 N ≈ 100k g e centro de gravidade em G 1 . Se ele tiver de suportar uma carga máxima de 1600N posicionada no ponto G 2 , determine o menor contrapeso W que dev
A haste uniforme de 30 N tem comprimento l = 1m . Se s = 1,5m , determine a distância h de posicionamento da extremidade A ao longo da parede lisa para que haja equilíbrio.
Se d = 1m e θ = 30 ° , determine a reação normal nos suportes lisos e a distância exigida a para a posição do rolete se P = 600N . Desconsidere o peso da haste.
A parte superior do guindaste consiste na lança A B , que é apoiada pelo pino em A , o cabo de sustentação B C e o cabo C D , cada cabo sendo preso separadamente ao mastro em C . Se a carga de 5 kN fo