Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 112
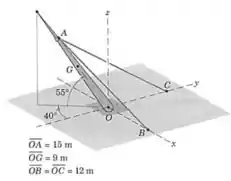
O mastro de , com centro de massa em , é mantido na posição mostrada por uma rótula em e por dois cabos e . Determine as forças trativas nos dois cabos e as componentes , e da força de reação em .
Passo 1
Vamos começar escrevendo as coordenadas do ponto , para então podermos escrever os vetores unitários nas direções de e .
E sabendo que :
E então, considerando que , os vetores nas direções mencionadas são:
E para encontrar os vetores unitários é só dividir pelo módulo:
E as formas vetoriais das trações são simplesmente e .
Passo 2
Agora vamos considerar as condições de equilíbrio para as forças na direção de cada eixo:
Ainda temos cinco variáveis, mas só três equações: não é suficiente!
Passo 3
Vamos procurar outras equações de equilíbrio. Se calcularmos o momento em relação ao eixo que une os pontos e nós vamos excluir as duas trações, e chegaremos em uama conta bem simples:
E para o momento em relação ao ponto só precisamos considerar a força peso e a componente da força em :
E o único vetor mais complicado de se escrever nessa equação é o que liga o ponto ao ponto :
A componente desse vetor seria só um trabalho a mais para calcular, já que vamos projetar no eixo de qualquer forma.
E vamos escrever esses produtos vetoriais como determinantes:
E agora falta fazer o produto interno com :
Beleza, agora podemos adicionar essa equação ao nosso sistema:
Passo 4
Ainda falta encontrar mais uma equação. Dessa vez vamos considerar o momento em relação ao eixo :
Nesse caso vamos eliminar todas as força em e a tração . Ficamos apenas com a componente em da tração e com a força peso:
E essa é a última equação do nosso sistema.
Passo 5
Ficamos então com as seguintes equações:
Agora é só resolver o sistema de baixo para cima para concluir o problema:
Pronto, já temos todas as respostas.
Resposta
As forças são , , , e .