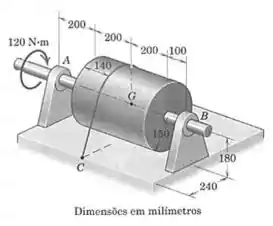
O tambor e o eixo estão soldados e têm uma massa de e centro de massa em . O eixo está submetido a um torque de e o tambor é impedido de girar pela corda firmemente enrolada em torno dele e presa ao ponto . Calcule os módulos das forças suportadas pelos mancais e .

Agora que conhecemos esse ângulo podemos começar a montar equações de equilíbrio. Primeiro precisamos definir alguns eixos e desenhar as forças:

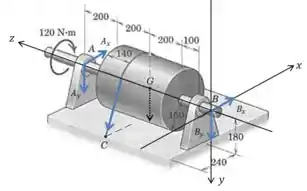
Vamos começar pensando no momento em relação ao eixo , porque nesse caso as forças em e , e o peso, terão momento nulo:

E agora vamos tentar reduzir esse problema a um caso bidimensional. Começamos pensando no plano -, essa é a vista “de cima” do sistema.

Nesse plano temos apenas as forças , , e uma componente de dada pela seguinte expressão:

Se calcularmos a equação de equilíbrio do momento em relação ao ponto , o momento de será nulo, então:

Agora, continuando no mesmo plano, vamos fazer o equilíbrio das forças na direção do eixo :

Em seguida vamos considerar outro plano, o -. Que corresponde à vista “de lado” do sistema, como se você estivesse em pé no lado positivo do eixo . Isso é um pouco mais complicado de visualizar, então vamos desenhar:

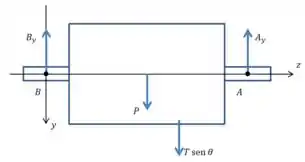
E agora vamos usar uma equação de equilíbrio do momento em relação ao ponto :

E por último podemos usar o equilíbrio das forças na direção :

E agora podemos calcular os módulos das duas forças: