Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 60

Estime o aumento no volume do taque do Problema 10.59 . Dica: Use os resultados do Problema 10.54 como confirmação.

Passo 1

Olá, galerinha! Tudo bem com vocês?

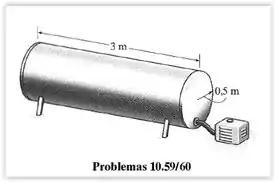
Para resolver esse problema você vai precisar dar uma olhada nos problemas 10.59 e 10.54 , pois usaremos informações fornecidas e/ou encontradas em ambos.

Vamos começar separando os dados informados no problema 10.59:

p = 15 ⋅ 10 6   P a

L = 3   m

r = 0,5   m

t = 0,01   m

E a ç o = 200   G P a

v a ç o = 0,3

Os resultados obtidos para o aumento do comprimento e do diâmentro do vaso de pressão cilíndrico foram:

Δ L = 0,00 225   m

Δ d = 0,00 31875   m

Sabendo que o raio é a metade do diâmetro, podemos calcular sua variação fazendo:

Δ r = Δ d 2

Δ r = 0,00 31875 2

Δ r = 0,00159375   m

Passo 2

Substituindo esses dados do problema 10.59 na equação que nos fornece a variação do volume do vaso de pressão cilíndrico, temos que:

Δ V = π ( r 2 Δ L + 2 r Δ r L )

Δ V = π ( 0,5 2 ⋅ 0,00225 + 2 ⋅ 0,5 ⋅ 0,00159375 ⋅ 3 )

Δ V = 0,016787   m 3

Passo 3

Vamos então confirmar essa resposta com o resultado obtido no problema 10.60 .

d V V = p r E t 2,5 - 2 v

Sendo que,

V = π r 2 L

Substituindo:

d V = p r E t 2,5 - 2 v ⋅ π r 2 L

d V = 15 ⋅ 10 6 ⋅ 0,5 200 ⋅ 10 9 ⋅ 0,01 2,5 - 2 ⋅ 0,3 ⋅ π ⋅ 0,5 2 ⋅ 3

d V = 15 ⋅ 10 6 ⋅ 0,5 200 ⋅ 10 9 ⋅ 0,01 2,5 - 2 ⋅ 0,3 ⋅ π ⋅ 0,5 2 ⋅ 3

d V = 0,016787   m 3

Resposta

Δ V = 0,016787   m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As extremidades do vaso de pressão cilíndrico são fechadas com tampas semiesféricas para reduzir a tensão de flexão que ocorreria se as tampas fossem planas. As tensões de flexão nas linhas de junção
Um vaso de pressão cilíndrico de parede fina tem raio interno r , espessura t e comprimento L . Se for submetido a uma pressão interna p , mostre que o aumento em seu raio interno é d r=r ϵ 1 =p r ² (
O tubo de aço A - 36 está sujeito à carga axial de 60k N . Determine a mudança no volume do material após a aplicação da carga.
Uma haste de latão de 8m m de diâmetro tem módulo de elasticidade E l a t =100G P a . Se a haste tiver 3m de comprimento e for submetida a uma carga axial de 2k N , determine seu alongamento. Qual ser
O parafuso de 8m m de diâmetro é feito de uma liga de alumínio e está instalado em uma luva de magnésio com diâmetro interno de 12m m e diâmetro externo de 20m m . Se os comprimentos originais do para