Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 12

A forma original de uma peça de plástico é retangular. Determine a deformação por cisalhamento γ x y nos cantos A e B se o plástico se distorcer como mostram as linhas tracejadas.

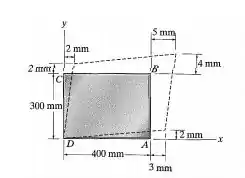
Passo 1

Falaa, a deformação por cilhamento é a variação angular nos vértices da nossa figura. Então a gente precisa achar cada um desses ângulos finais e substrair de 90 °   ( π / 2 ) (ângulo inicial dos vértices).

Primeiro, vamos esquematizar a situação:

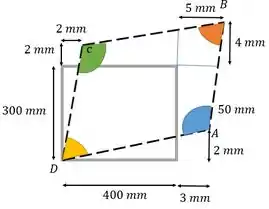
Pelo desenho, temos que:

∆ A x = 3 m m

∆ C x = 2 m m

∆ B x = 5 m m

∆ A y = 2 m m

∆ C y = 2 m m

∆ B y = 4 m m

Passo 2

Agora, basta aplicar geometria. Repara:

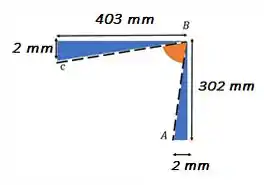
Por essa figura, podemos ver que o ângulo de B forma 90 ° com os ângulos em B desses dois triângulos. Então podemos fazer:

B ^ = π 2 - a r c t a n 2 302 - a r c t a n 2 40 3 = 1,5 5921

Passo 3

Bora para A . Podemos fazer algo parecido:

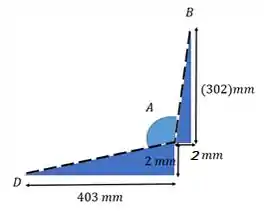
Vemos que o ângulo em A forma 270 ° com os outros ângulos em A dos triângulos:

A ^ = 2 π - π 2 - a r c t a n 403 2 - arctan ⁡ 302 2 = 1,5 8238

Passo 4

Por fim, basta calcular a deformação pedida:

γ x y B = π 2 - 1,55921 = 11,586 × 10 - 3   r a d

γ x y A = π 2 - 1,5 8238 = - 11,583 × 10 - 3   r a d

Veja que a resposta precisa ser em rad, ok?

Resposta

γ x y B = 11,586 × 10 - 3   r a d

γ x y A = - 11,583 × 10 - 3   r a d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

uma haste de poliestireno consiste em duas partes cilíndricas AB e BC engastadas em ambas as extremidades e suportando duas ações de 6 kip conforme mostrado. Sabendo que E = 0,45x10 6 p s i . Determin
Três barras de aço ( E = 29x10 6p s i ) suportam uma carga P de 8,5 - k i p . Cada uma das barras AB e CD tem uma área de seção transversal de 0,32 - i n ² ², e a barra EF tem uma área de seção transv
A barra rígida AD é suportada por dois cabos de aço com 1/16 in. de diâmetro ( E = 29x10 6p s i ) e por um pino e um suporte em D. Sabendo que os cabos foram inicialmente tensionados, determine (a) a
Resolva o Problema 2.41 supondo que a barra AC é feita de latão e a barra CE é feita de aço.
Cada uma das hastes BD e CE é feita de latão ( E = 105G P a ) e tem área de seção transversal de 200mm². Determine a deflexão da extremidade A do elemento rígido ABC provocada pela ação de 2 kN.