Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 47
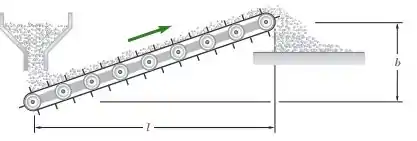
Uma fórmula para especificação de potência deve ser deduzida para os motores elétricos que acionam esteiras transportadoras que deslocam material sólido a diferentes taxas ao longo de alturas e distâncias diferentes. Representando por a eficiência dos motores e desprezando a potência necessária para acionar a própria esteira, deduza uma fórmula para a potência em em termos da vazão em massa em , da altura e da distância horizontal Em metros.
Passo 1
Vamos lá! Precisamos obter a relação para a potência do motor necessário para acionar a esteira transportadora. Mas antes de nos preocuparmos com a questão de eficiência, vamos calcular aqui a potência útil, aquela que realmente é utilizada!
Sabemos que a potência é a taxa de variação do trabalho de uma força no tempo. Portanto,
Como a força atuante é a força peso (em uma altura de elevação), temos:
Portanto,
Esta é a nossa relação para o cálculo da potência!
Passo 2
Agora que obtivemos a relação da potência, precisamos transformar as unidades para atender o enunciado da questão e conseguirmos ela em kW.
Para isto, vamos colocar todas as incógnitas no SI (sistema internacional).
Como nada foi dito sobre a gravidade e o comprimento foi dado em metros, não precisamos mexer aqui. Assim, a única operação que precisamos nos preocupar é com a taxa de variação de massa.
Aqui devemos ter bastante cuidado! No enunciado da questão ele pede para escrever como ,o que normalmente é apenas a massa, e aqui escrevemos como apenas para diferenciar.
Além disto, esta taxa está em , sendo que deveria estar em . Portanto,
Então, chamando de e fazendo a substituição, a potência útil em será:
Como queremos em , precisamos dividir por . Logo,
Passo 3
Só que temos um problema. No final do Passo 2 nós calculamos a potência útil. Entretanto, a questão nos pede para calcularmos a potência do motor! Lembrando a definição, ela será: